
【题目】如图统计了截止2019年年底中国电动车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
中国电动车充电桩细分产品占比情况:
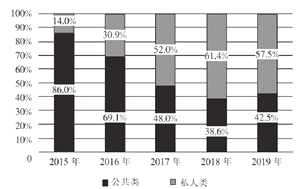
中国电动车充电桩细分产品保有量情况:(单位:万台)
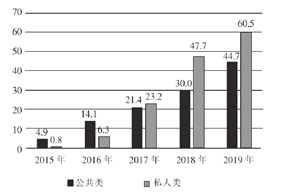
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过![]()
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且(2b﹣c)cosA=acosC.
(1)求A;
(2)若△ABC的面积为![]() ,求a的最小值.
,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,PA=PD=AD=2,BC=1,![]() .
.
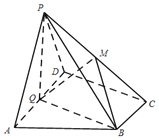
(1)求证:平面PQB⊥平面PAD;
(2)若M是棱PC上的一点,且满足![]() ,求二面角M﹣BQ﹣C的大小.
,求二面角M﹣BQ﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交
交![]() 两点,
两点,![]() 是坐标原点,分别过点
是坐标原点,分别过点![]() 作
作![]() ,
,![]() 的平行线,两平行线的交点刚好在椭圆
的平行线,两平行线的交点刚好在椭圆![]() 上,判断
上,判断![]() 是否为定值?若为定值,求出该定值;若不是,请说明理由.
是否为定值?若为定值,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点.设直线
两点.设直线![]() 是抛物线
是抛物线![]() 的切线,且直线
的切线,且直线![]() 为
为![]() 上一点,且
上一点,且![]() 的最小值为
的最小值为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设![]() 是抛物线
是抛物线![]() 上,分别位于
上,分别位于![]() 轴两侧的两个动点,
轴两侧的两个动点,![]() 为坐标原点,且
为坐标原点,且![]() .求证:直线
.求证:直线![]() 必过定点,并求出该定点的坐标.
必过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据气象部门预报,在距离某个码头A南偏东45°方向的600km处的热带风暴中心B正以30km/h的速度向正北方向移动,距离风暴中心450km以内的地区都将受到影响,从现在起经过___小时后该码头A将受到热带风暴的影响(精确到0.01).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究55岁左右的中国人睡眠质量与心脑血管病是否有关联,某机构在适龄人群中随机抽取了100万个样本,调查了他们每周是否至少三个晚上出现了三种失眠症状,![]() 症状:入睡困难;
症状:入睡困难;![]() 症状:醒得太早;
症状:醒得太早;![]() 症状:不能深度入睡或做梦,得到的调查数据如下:
症状:不能深度入睡或做梦,得到的调查数据如下:
数据1:出现![]() 症状人数为8.5万,出现
症状人数为8.5万,出现![]() 症状人数为9.3万,出现
症状人数为9.3万,出现![]() 症状人数为6.5万,其中含
症状人数为6.5万,其中含![]() 症状同时出现1.8万人,
症状同时出现1.8万人,![]() 症状同时出现1万人,
症状同时出现1万人,![]() 症状同时出现2万人,
症状同时出现2万人,![]() 症状同时出现0.5万人;
症状同时出现0.5万人;
数据2:同时有失眠症状和患心脑血管病的人数为5万人,没有失眠症状且无心脑血管病的人数为73万人.
(Ⅰ)依据上述数据试分析55岁左右的中国人患有失眠症的比例大约多少?
(Ⅱ)根据以上数据完成如下列联表,并根据所填列联表判断能否有95%的把握说明失眠与心脑血管病存在“强关联”?
失眠 | 不失眠 | 合计 | |
患心脑血管疾病 | |||
不患心脑血管疾病 | |||
合计 |
参考数据如下:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: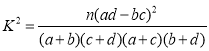
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com