
【题目】某公司采购了一批零件,为了检测这批零件是否合格,从中随机抽测120个零件的长度(单位:分米),按数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这6组,得到如图所示的频率分布直方图,其中长度大于或等于1.59分米的零件有20个,其长度分别为1.59,1.59,1.61,1.61,1.62,1.63,1.63,1.64,1.65,1.65,1.65,1.65,1.66,1.67,1.68,1.69,1.69,1.71,1.72,1.74,以这120个零件在各组的长度的频率估计整批零件在各组长度的概率.
这6组,得到如图所示的频率分布直方图,其中长度大于或等于1.59分米的零件有20个,其长度分别为1.59,1.59,1.61,1.61,1.62,1.63,1.63,1.64,1.65,1.65,1.65,1.65,1.66,1.67,1.68,1.69,1.69,1.71,1.72,1.74,以这120个零件在各组的长度的频率估计整批零件在各组长度的概率.
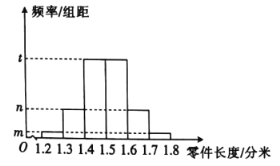
(1)求这批零件的长度大于1.60分米的频率,并求频率分布直方图中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若从这批零件中随机选取3个,记![]() 为抽取的零件长度在
为抽取的零件长度在![]() 的个数,求
的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() 满足近似于正态分布
满足近似于正态分布![]() 的概率分布.如果这批零件的长度
的概率分布.如果这批零件的长度![]() (单位:分米)满足近似于正态分布
(单位:分米)满足近似于正态分布![]() 的概率分布,则认为这批零件是合格的将顺利被签收;否则,公司将拒绝签收.试问,该批零件能否被签收?
的概率分布,则认为这批零件是合格的将顺利被签收;否则,公司将拒绝签收.试问,该批零件能否被签收?
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)分布列见解析,2.1;(3)能被该公司签收.
;(2)分布列见解析,2.1;(3)能被该公司签收.
【解析】
(1)根据120件样本零件中长度大于1.60分米的共有18件即可求出频率,根据所给数据分别求出![]() ,
,![]() 两组的频率可得m,n,再根据频率之和为1求出t即可;
两组的频率可得m,n,再根据频率之和为1求出t即可;
(2)由题意从这批零件中随机选取1件,长度在![]() 的概率
的概率![]() ,且服从二项分布,即可求解;、
,且服从二项分布,即可求解;、
(3)根据题意,验证零件数据对于![]() 且
且![]() 是否成立即可求解.
是否成立即可求解.
(1)由题意可知120件样本零件中长度大于1.60分米的共有18件,
则这批零件的长度大于1.60分米的频率为![]() ,
,
记![]() 为零件的长度,则
为零件的长度,则![]() ,
,
![]() ,
,
![]() ,
,
故![]() ,
,![]() ,
,![]() .
.
(2)由(1)可知从这批零件中随机选取1件,长度在![]() 的概率
的概率![]() .
.
且随机变量![]() 服从二项分布
服从二项分布![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
故随机变量![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
| 0.027 | 0.189 | 0.441 | 0.343 |
![]() (或
(或![]() ).
).
(3)由题意可知![]() ,
,![]() ,
,
则![]() ;
;
![]() ,
,
因为![]() ,
,![]() ,
,
所以这批零件的长度满足近似于正态分布![]() 的概率分布.
的概率分布.
应认为这批零件是合格的,将顺利被该公司签收.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,四点
,四点![]() ,
,![]() ,
,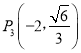 ,
,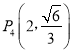 中恰有三个点在椭圆C上,左、右焦点分别为F1、F2.
中恰有三个点在椭圆C上,左、右焦点分别为F1、F2.
(1)求椭圆C的方程;
(2)过左焦点F1且不平行坐标轴的直线l交椭圆于P、Q两点,若PQ的中点为N,O为原点,直线ON交直线x=﹣3于点M,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为原点,抛物线![]() 的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
(1)求C的方程;
(2)过C的焦点F作直线l与抛物线C交于A,B两点,若以AH为直径的圆过B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为直角梯形,AB//CD,
中,底面ABCD为直角梯形,AB//CD,![]()
![]() 是以
是以![]() 为斜边的等腰直角三角形,且平面
为斜边的等腰直角三角形,且平面![]() 平面ABCD,点F满足,
平面ABCD,点F满足,![]() .
.
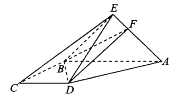
(1)试探究![]() 为何值时,CE//平面BDF,并给予证明;
为何值时,CE//平面BDF,并给予证明;
(2)在(1)的条件下,求直线AB与平面BDF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点
的左焦点![]() ,点
,点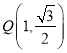 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)经过圆![]() :
:![]() 上一动点
上一动点![]() 作椭圆
作椭圆![]() 的两条切线,切点分别记为
的两条切线,切点分别记为![]() ,
,![]() ,直线
,直线![]() ,
,![]() 分别与圆
分别与圆![]() 相交于异于点
相交于异于点![]() 的
的![]() ,
,![]() 两点.
两点.
(i)当直线![]() ,
,![]() 的斜率都存在时,记直线
的斜率都存在时,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .求证:
.求证:![]() ;
;
(ii)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】发展“会员”、提供优惠,成为不少实体店在网购冲击下吸引客流的重要方式.某连锁店为了吸引会员,在2019年春节期间推出一系列优惠促销活动.抽奖返现便是针对“白金卡会员”、“金卡会员”、“银卡会员”、“基本会员”不同级别的会员享受不同的优惠的一项活动:“白金卡会员”、“金卡会员”、“银卡会员”、“基本会员”分别有4次、3次、2次、1次抽奖机会.抽奖机如图:抽奖者第一次按下抽奖键,在正四面体的顶点![]() 出现一个小球,再次按下抽奖键,小球以相等的可能移向邻近的顶点之一,再次按下抽奖键,小球又以相等的可能移向邻近的顶点之一……每一个顶点上均有一个发光器,小球在某点时,该点等可能发红光或蓝光,若出现红光则获得2个单位现金,若出现蓝光则获得3个单位现金.
出现一个小球,再次按下抽奖键,小球以相等的可能移向邻近的顶点之一,再次按下抽奖键,小球又以相等的可能移向邻近的顶点之一……每一个顶点上均有一个发光器,小球在某点时,该点等可能发红光或蓝光,若出现红光则获得2个单位现金,若出现蓝光则获得3个单位现金.
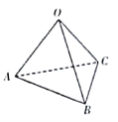
(1)求“银卡会员”获得奖金的分布列;
(2)![]() 表示第
表示第![]() 次按下抽奖键,小球出现在
次按下抽奖键,小球出现在![]() 点处的概率.
点处的概率.
①求![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
②写出![]() 与
与![]() 关系式,并说明理由.
关系式,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.
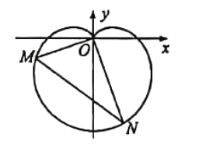
(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
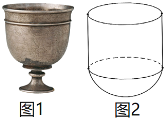
【题目】唐朝的狩猎景象浮雕银杯如图1所示.其浮雕临摹了国画、漆绘和墓室壁画,体现了古人的智慧与工艺.它的盛酒部分可以近似地看作是半球与圆柱的组合体(假设内壁表面光滑,忽略杯壁厚度),如图2所示.已知球的半径为R,酒杯内壁表面积为![]() ,设酒杯上部分(圆柱)的体积为
,设酒杯上部分(圆柱)的体积为![]() ,下部分(半球)的体积为
,下部分(半球)的体积为![]() ,则
,则![]() ( )
( )
A.2B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com