
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】(Ⅰ)由已知,点C,D的坐标分别为(0,-b),(0,b)
又点P的坐标为(0,1),且![]() =-1
=-1
于是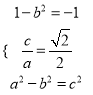 ,解得a=2,b=
,解得a=2,b=![]()
所以椭圆E方程为![]() .
.
(Ⅱ)当直线AB斜率存在时,设直线AB的方程为y=kx+1
A,B的坐标分别为(x1,y1),(x2,y2)
联立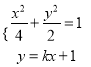 ,得(2k2+1)x2+4kx-2=0
,得(2k2+1)x2+4kx-2=0
其判别式△=(4k)2+8(2k2+1)>0
所以![]()
从而![]() =x1x2+y1y2+λ[x1x2+(y1-1)(y2-1)]
=x1x2+y1y2+λ[x1x2+(y1-1)(y2-1)]
=(1+λ)(1+k2)x1x2+k(x1+x2)+1
=![]()
=-![]()
所以,当λ=1时,-![]() =-3
=-3
此时, ![]() =-3为定值
=-3为定值
当直线AB斜率不存在时,直线AB即为直线CD
此时![]() =-2-1=-3
=-2-1=-3
故存在常数λ=-1,使得![]() 为定值-3.
为定值-3.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足: ![]() ,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1).
,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1).
(1)求数列{an},{bn}的通项公式
(2)证明:数列{bn}中的任意三项不可能成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家发现视觉和空间能力与性别有关,孝感市黄陂路高中数学兴趣小组为了验证这个结论,从兴趣小组中抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)

(1)能否据此判断有![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)以上列联表中女生选做几何题的频率作为概率,从该校1500名女生中随机选6名女生,记6名女生选做几何题的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() 和方差
和方差![]() .
.
附表:

参考公式: 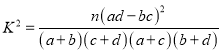 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,∠BAD=120°,对角线AC与BD交于点O,M为OC中点. 
(1)求证:BD⊥PM
(2)若二面角O﹣PM﹣D的正切值为2 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙H被直线x-y-1=0,x+y-3=0分成面积相等的四个部分,且截x轴所得线段的长为2。
(I)求⊙H的方程;
(Ⅱ)若存在过点P(0,b)的直线与⊙H相交于M,N两点,且点M恰好是线段PN的中点,求实数b的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1(侧棱垂直于底面的棱柱为直棱柱)中,BC=CC1=1,AC=2,∠ABC=90°. 
(1)求证:平面ABC1⊥平面A1B1C;
(2)设D为AC的中点,求平面ABC1与平面C1BD所成锐角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区提倡低碳生活,环保出行,在小区提供自行车出租![]() 该小区有40辆自行车供小区住户租赁使用,管理这些自行车的费用是每日92元,根据经验,若每辆自行车的日租金不超过5元,则自行车可以全部出租,若超过5元,则每超过1元,租不出的自行车就增加2辆,为了便于结算,每辆自行车的日租金x元只取整数,用
该小区有40辆自行车供小区住户租赁使用,管理这些自行车的费用是每日92元,根据经验,若每辆自行车的日租金不超过5元,则自行车可以全部出租,若超过5元,则每超过1元,租不出的自行车就增加2辆,为了便于结算,每辆自行车的日租金x元只取整数,用![]() 元表示出租自行车的日纯收入
元表示出租自行车的日纯收入![]() 日纯收入
日纯收入![]() 一日出租自行车的总收入
一日出租自行车的总收入![]() 管理费用
管理费用![]()
![]() 求函数
求函数![]() 的解析式及其定义域;
的解析式及其定义域;
![]() 当租金定为多少时,才能使一天的纯收入最大?
当租金定为多少时,才能使一天的纯收入最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com