Question

20．用向量证明：若平面内的一条直线垂直于平面外的一条直线在该平面上的投影，则这两条直线垂直．

Answer 1

分析 画出图形，根据条件，只需把直线表示出向量，利用向量的数量积为0，证明垂直．

解答 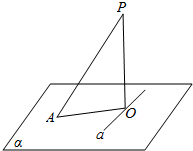证明：如图，PA、PO分别是平面α的垂线、斜线，AO是PA在平面α内的射影，
设直线a上非零向量$\overrightarrow{a}$，要证a⊥OA⇒a⊥PA，
即证$\overrightarrow{a}$•$\overrightarrow{OA}$=0⇒$\overrightarrow{a}$•$\overrightarrow{PA}$=0．
∵a?α，$\overrightarrow{a}$•$\overrightarrow{PO}$=0，
∵$\overrightarrow{a}$•$\overrightarrow{PA}$=$\overrightarrow{a}$•（$\overrightarrow{PO}$+$\overrightarrow{OA}$）=$\overrightarrow{a}$•$\overrightarrow{PO}$+$\overrightarrow{a}$•$\overrightarrow{OA}$=0+0=0．
∴a⊥PA．

点评 本题考查三垂线定理，考查向量的数量积，考查学生计算能力，属于中档题．