练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数f（x）=sin（2x+ ）+tan cos2x．
    （1）求f（x）的最小正周期及其图象的对称轴方程；
    （2）求函数f（x）在区间（0， ）上的值域．

    【答案】
    （1）解：f（x）= sin 2x+ cos 2x﹣ cos 2x= sin 2x+ cos 2x=

    所以f（x）的最小正周期为T= =π

    令2x+ =kπ+ （k∈Z），

    得对称轴方程为x= + （k∈Z）．


    （2）解：∵f（x）= ， ，

    ∴2x∈（0，π），

    则 ，

    ∴f（x）的值域为


    【解析】（1）利用两角和的正弦公式化简解析式，由三角函数的周期公式求出f（x）的最小正周期，由正弦函数图象的对称轴方程，求出图象的对称轴方程；（2）由x的范围求出 的范围，由正弦函数的性质求出函数f（x）的值域．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】[选修4―4：坐标系与参数方程]

    在直角坐标系xOy中，直线l1的参数方程为（t为参数），直线l2的参数方程为.设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．

    （1）写出C的普通方程；

    （2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ(cosθ+sinθ) =0，M为l3与C的交点，求M的极径.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用数学归纳法证明：12﹣22+32﹣42+…+（﹣1）n﹣1n2=（﹣1）n﹣1 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线，直线倾斜角是且过抛物线的焦点，直线被抛物线截得的线段长是16，双曲线： 的一个焦点在抛物线的准线上，则直线与轴的交点到双曲线的一条渐近线的距离是（ ）

    A. 2 B. C. D. 1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知| |=4，| |=8，| |=4 ．
    （1）计算：① ，②|4 ﹣2 |
    （2）若（ +2 ）⊥（k ﹣ ），求实数k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知O为坐标原点，向量 =（sinα，1）， =（cosα，0）， =（﹣sinα，2），点P是直线AB上的一点，且 = ．
    （1）若O，P，C三点共线，求tanα的值；
    （2）在（Ⅰ）条件下，求 +sin2α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某调查机构对本市小学生课业负担情况进行了调查，设平均每人每天做作业的时间为x分钟．有1000名小学生参加了此项调查，调查所得数据用程序框图处理，若输出的结果是680，则平均每天做作业的时间在0～60分钟内的学生的频率是（ ）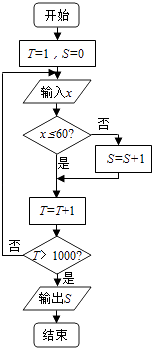

    A.680
    B.320
    C.0.68
    D.0.32

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中，且。

    （1）当时，求函数的单调区间；

    （2）设，若存在极大值，且对于的一切可能取值， 的极大值均小于0，求的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C的参数方程为 ( 为参数)，以直角坐标系原点为极点，Ox轴正半轴为极轴建立极坐标系．
    （1）求曲线C的极坐标方程;
    （2）若直线l的极坐标方程为 ，求直线l被曲线C截得的弦长.

    查看答案和解析>>

    同步练习册答案