
����Ŀ��ijУ�ӲμӸ���ģ�⿼�Ե�ѧ���������ȡ60��ѧ����������ѧ�ɼ�(��Ϊ����)�ֳ�����[90,100)��[100,110)������[140,150)��õ����²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺
�������[120,130)�ڵ�Ƶ�ʣ�����ȫ���Ƶ
�ʷֲ�ֱ��ͼ��
ͳ�Ʒ����У�ͬһ�����ݳ��ø���������е�
ֵ��Ϊ�������ݴ˹��Ʊ��ο��Ե�ƽ���֣�
(3)�÷ֲ�����ķ����ڷ�����Ϊ[110,130)��ѧ���г�ȡһ������Ϊ6��������������������һ�����壬������ȡ2������������1���ڷ�����[120,130)�ڵĸ��ʣ�

���𰸡�(1)�������ʾ��(2)121��(3) ![]()
�������������������1��Ƶ�ʷֲ�ֱ��ͼ�У�С���ε����������һ���Ƶ�ʣ���Ƶ�ʵĺ͵���1�������������![]() �ڵ�Ƶ�ʣ�����������εĸߣ�����ͼ������2��ͬһ�����ݳ��ø���������е�ֵ��Ϊ���������е�ֵ��ÿһ���Ƶ�������������ǵĺͼ���������ο��Ե�ƽ���֣���3���ȼ���
�ڵ�Ƶ�ʣ�����������εĸߣ�����ͼ������2��ͬһ�����ݳ��ø���������е�ֵ��Ϊ���������е�ֵ��ÿһ���Ƶ�������������ǵĺͼ���������ο��Ե�ƽ���֣���3���ȼ���![]() ��
��![]() �����ε�������Ȼ���ձ������г�ȡ�������������ȡ2�ˣ�������1���ڷ�����
�����ε�������Ȼ���ձ������г�ȡ�������������ȡ2�ˣ�������1���ڷ�����![]() Ϊ�¼�
Ϊ�¼�![]() ��Ȼ���г������¼��ռ�����Ļ����¼����Լ��¼�
��Ȼ���г������¼��ռ�����Ļ����¼����Լ��¼�![]() �����Ļ����¼���������¼��ĸ��������Ŀ��ֵ����.
�����Ļ����¼���������¼��ĸ��������Ŀ��ֵ����.
���������(1)������[120,130)�ڵ�Ƶ��Ϊ��1��(0.1��0.15��0.15��0.25��0.05)��1��0.7��0.3�� ![]() ����ȫ���ֱ��ͼ���£�
����ȫ���ֱ��ͼ���£�
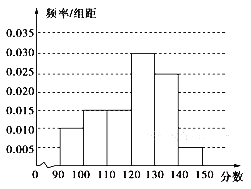
(2)ƽ����Ϊ��95��0.1��105��0.15��115��0.15��125��0.3��135��0.25��145��0.05��121.
(3)�����⣬[110,120)�����ε�����Ϊ��60��0.15��9�ˣ�[120,130)�����ε�����Ϊ��60��0.3��18�ˣ�
���÷ֲ�����ķ����ڷ�����Ϊ[110,130)��ѧ���г�ȡһ������Ϊ6��������
������[110,120)�������ڳ�ȡ2�ˣ����ֱ��Ϊm��n��
��[120,130)�������ڳ�ȡ4�˲��ֱ��Ϊa��b��c��d��
�衰����������ȡ2�ˣ�������1���ڷ�����[120,130)�ڡ�Ϊ�¼�A��������¼��У�(m��n)��(m��a)��(m��b)��(m��c)��(m��d)��(n��a)��(n��b)��(n��c)��(n��d)��(a��b)��(a��c)��(a��d)��(b��c)��(b��d)��(c��d)��15�֣�
�¼�A�����Ļ����¼��У�(m��n)��(m��a)��(m��b)��(m��c)��(m��d)��(n��a)��(n��b)��(n��c)��(n��d)��9�֣���![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У���֪
�У���֪![]() ��
��![]() ����
����![]() �� ��
�� ��
A. ����ֱ�������� B. �ȱ�������
C. ��Ƿǵȱ������� D. �۽�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-5������ʽѡ��
��֪����f��x��=log2��|x+1|+|x��2|��m����
��1����m=7ʱ������f��x���Ķ�����
��2��������x�IJ���ʽf��x����2�Ľ⼯��R����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������![]() ��,����
��,����![]() �DZ߳�Ϊ2��������,����
�DZ߳�Ϊ2��������,����![]() �ǵ���ֱ��������,��
�ǵ���ֱ��������,��![]() ,����
,����![]() �͵���
�͵���![]() .
.
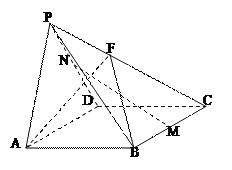
(1)��![]() �ֱ�Ϊ��
�ֱ�Ϊ��![]() ���е�,��֤:
���е�,��֤:![]() ��ƽ��
��ƽ��![]() ��
��
(2)��![]() ���Ƿ����һ��
���Ƿ����һ��![]() ,ʹ�����
,ʹ�����![]() ��
��![]() �ǣ�������,���
�ǣ�������,���![]() �ij�����������,��˵������.
�ij�����������,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�AD��BC����ADC=��PAB=90�㣬BC=CD= ![]() AD��EΪ��AD���е㣬����ֱ��PA��CD���ɵĽ�Ϊ90�㣮
AD��EΪ��AD���е㣬����ֱ��PA��CD���ɵĽ�Ϊ90�㣮 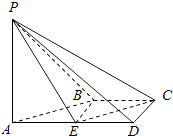
��1����ƽ��PAB����һ��M��ʹ��ֱ��CM��ƽ��PBE����˵�����ɣ�
��2���������P��CD��A�Ĵ�СΪ45�㣬��ֱ��PA��ƽ��PCE���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У���
�У���![]() Ϊ���㣬
Ϊ���㣬![]() ��������Ϊ���Ὠ��������ϵ������
��������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ������
������![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������.
������.
(1)������![]() ��ֱ�����귽�̣�����
��ֱ�����귽�̣�����![]() �ļ����귽�̡�
�ļ����귽�̡�
(2)������![]() ������
������![]() ������������ʱ����ʵ��
������������ʱ����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߳�Ϊ ![]() ������ABCD�У���BAD=60�㣬�ضԽ���BD�۳ɶ����A��BD��CΪ120���������ABCD����������������ı����Ϊ�� ��
������ABCD�У���BAD=60�㣬�ضԽ���BD�۳ɶ����A��BD��CΪ120���������ABCD����������������ı����Ϊ�� ��
A.25��
B.26��
C.27��
D.28��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��ͼ�����
��ͼ�����![]() ��������
��������![]() ����
����![]() ��������СֵΪ
��������СֵΪ![]()
![]()
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2������![]() ������[0,1]�ϵ���Сֵ������
������[0,1]�ϵ���Сֵ������![]() ��
��
��3��������[��1,3]�ϣ�![]() ��ͼ����ں���
��ͼ����ں���![]() ��ͼ���Ϸ�����ȷ��ʵ��
��ͼ���Ϸ�����ȷ��ʵ��![]() �ķ�Χ��
�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���֪����f��x��=![]()
��1���жϺ���������[1,+�����ϵĵ�����,���ö���֤����Ľ��ۣ�
��2����ú���������[1,4]�ϵ����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com