(本小题满分12分)设函数
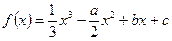
,其中
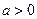
,曲线
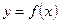
在点
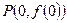
处的切线方程为
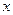
轴
(1)若
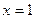
为
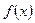
的极值点,求
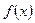
的解析式
(2)若过点

可作曲线
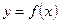
的三条不同切线,求
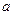
的取值范围。
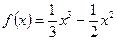
,
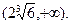
解:由
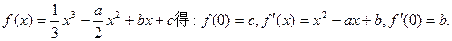
又由曲线
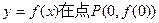
处的切线方程为
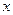
轴,得
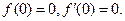
故
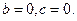
…………………………… 2分
(I)又
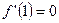
,所以
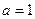
,
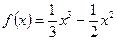
…………………………… 4分
(II)
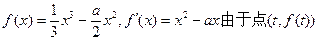
处的切线方程为
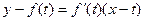
,而点(0,2)在切线上,所以
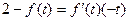
,
化简得

……………… 6分
过点(0,2)可作
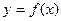
的三条切线,等价于方程
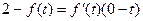
有三个相异的实根,即等价于方程
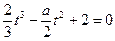
有三个相异的实根.
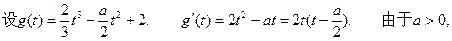
故有
由
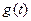
的单调性知:要使
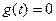
有三个相异的实根,当且仅当
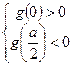
时满足,即
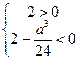
,

.
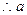
的取值范围是
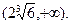
……………………………………………… 12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(12分)已知函数
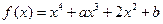
(
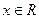
),其中
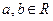
.
(Ⅰ)当
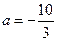
时,讨论函数
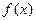
的单调性;
(Ⅱ)若函数
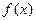
仅在
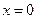
处有极值,求
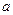
的取值范围;
(Ⅲ)若对于任意的
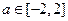
,不等式
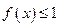
在
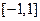
上恒成立,求
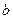
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
已知函数
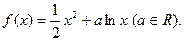
(1)若
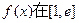
上

是增函数,求
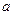
的取值范围;
(2)若
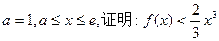
;
(3)若
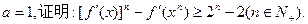
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数

(I)求函数
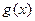
的单调递增区间;
(II)若
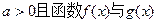
的图像有公共点,且在该点处的切线相同,用
a表示
b,并求
b的最大值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
f(x)=
x3,

=6,则
x0=( )
查看答案和解析>>

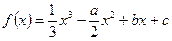 ,其中
,其中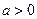 ,曲线
,曲线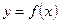 在点
在点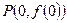 处的切线方程为
处的切线方程为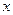 轴
轴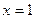 为
为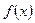 的极值点,求
的极值点,求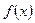 的解析式
的解析式 可作曲线
可作曲线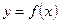 的三条不同切线,求
的三条不同切线,求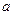 的取值范围。
的取值范围。 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 (
(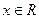 ),其中
),其中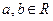 .
.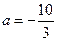 时,讨论函数
时,讨论函数 的单调性;
的单调性; 仅在
仅在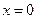 处有极值,求
处有极值,求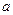 的取值范围;
的取值范围;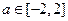 ,不等式
,不等式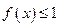 在
在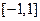 上恒成立,求
上恒成立,求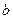 的取值范围.
的取值范围.