
某公司计划2013年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元.
【解析】设公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟,总收益为z元.由题意,得 目标函数为z=3000x+2000y.
目标函数为z=3000x+2000y.
二元一次不等式组等价于
作出二元一次不等式组所表示的平面区域,即可行域.
作直线l:3000x+2000y=0,即3x+2y=0.
联立 解得x=100,y=200.记点M的坐标为(100,200).
解得x=100,y=200.记点M的坐标为(100,200).
平移直线l,易知,当直线l过M点时,目标函数取得最大值.
∴zmax=3000x+2000y=700000(元).
答:该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元.


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第四章第2课时练习卷(解析版) 题型:解答题
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD∶DB=BE∶EC=2∶1,AE与CD交于P.设存在λ和μ使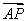 =λ
=λ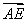 ,
,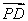 =μ
=μ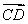 ,
,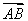 =a,
=a,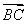 =b.
=b.
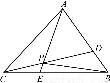
(1) 求λ及μ;
(2) 用a、b表示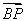 ;
;
(3) 求△PAC的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第4课时练习卷(解析版) 题型:填空题
设变量x,y满足|x|+|y|≤1,则x+2y的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第2课时练习卷(解析版) 题型:填空题
直线2x+y-10=0与不等式组 表示的平面区域的公共点有______个.
表示的平面区域的公共点有______个.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第1课时练习卷(解析版) 题型:解答题
某商场若将进货单价为8元的商品按每件10元出售,每天可销售100件,现准备采用提高售价,减少进货量的办法来增加利润,已知这种商品每件销售价提高1元,销售量就要减少10件,问该商场将销售价每件定为多少元时,才能使得每天所赚的利润最多?销售价每件定为多少元时,才能保证每天所赚的利润在300元以上?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:填空题
若等腰直角三角形的直角边长为2,则以一直角边所在的直线为轴旋转一周所成的几何体体积是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com