
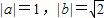 ,且
,且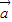 ⊥(
⊥( 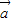 +
+ ),则向量
),则向量 与向量
与向量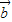 夹角的大小是 ;向量
夹角的大小是 ;向量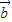 在向量
在向量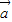 上的投影是 .
上的投影是 . 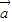 ⊥(
⊥( +
+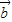 ),数量积为零,得到关于
),数量积为零,得到关于 与
与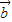 数量积的方程,解出结果代入求夹角的公式,注意夹角的范围,根据投影的定义,应用公式|
数量积的方程,解出结果代入求夹角的公式,注意夹角的范围,根据投影的定义,应用公式| |cos<
|cos< ,
,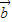 >=
>=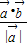 求解.
求解. |=1,|
|=1,|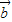 |=2,
|=2, ⊥(
⊥(  +
+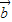 ),
),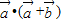 =0,
=0,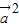 +
+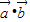 =0,
=0,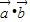 =-
=- =-1,
=-1, >=
>= =-
=- ,
,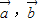 >∈[0°,180°],
>∈[0°,180°],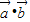 =-
=-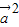 =-1,
=-1,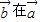 上的投影为
上的投影为 ,
,

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011年安徽省安庆市高一三校联考数学试卷 题型:解答题
已知函数 且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在
且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在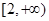 上的单调性?并证明你的结论.
上的单调性?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com