Question

6．已知函数$f（x）=\frac{a+lnx}{x}$，曲线f（x）在点（e，f（e））处的切线与直线y=e²x+e垂直．
（1）求a的值及f（x）的极值；
（2）是否存在区间$（{t，t+\frac{2}{3}}）（t＞0）$，使函数f（x）在此区间上存在极值和零点？若存在，求实数t的取值范围，若不存在，请说明理由；
（3）若不等式x²f（x）＞k（x-1）对任意x∈（1，+∞）恒成立，求整数k的最大值．

Answer 1

分析 （1）求出函数的导数，计算f（e），f′（e）的值，求出a的值，从而求出f（x）的解析式，求出函数的单调区间，得到函数的极值即可；
（2）画出函数f（x）的图象，结合图象求出t的范围即可；
（3）问题可化为$k＜\frac{x（1+lnx）}{x-1}$，令$h（x）=\frac{x（1+lnx）}{x-1}$，（x＞1），根据函数的单调性求出k的最大值即可．

解答 解：（1）由$f（x）=\frac{a+lnx}{x}$，得$f'（x）=\frac{1-a-lnx}{x^2}$．
因为f（x）在点（e，f（e））处的切线与直线y=e²x+e垂直，
所以$f'（e）=\frac{1-a-lne}{e^2}=\frac{-a}{e^2}=-\frac{1}{e^2}$，解得a=1，
所以$f（x）=\frac{1+lnx}{x}（x＞0）$，令$f'（x）=-\frac{lnx}{x^2}=0$，得x=1．
因为当x∈（0，1）时，f'（x）＞0，当x∈（1，+∞）时，f'（x）＜0
所以f（x）在（0，1）上单调递增，在（1，+∞）上单调递减，
故f（x）在x=1处取得极大值1，无极小值；
（2）因为f（x）在（1，+∞）上单调递减，且f（x）＞0
又由（1）知f（x）在（0，1）上单调递增，且$f（{e^{-2}}）=\frac{{1+ln{e^{-2}}}}{{{e^{-2}}}}=-{e^2}＜0$，f（1）=1＞0
所以由零点存在原理得f（x）在区间（0，1）存在唯一零点，函数f（x）的图象如图所示：
因为函数f（x）在区间$（{t，t+\frac{2}{3}}）（t＞0）$上存在极值和零点，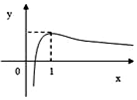

所以由$\left\{\begin{array}{l}0＜t＜1＜t+\frac{2}{3}\\ f（t）=\frac{1+lnt}{t}＜0\end{array}\right.$，解得$\frac{1}{3}＜t＜\frac{1}{e}$．
所以存在符合条件的区间，实数t的取值范围为$（{\frac{1}{3}，\frac{1}{e}}）$；
（3）当x∈（1，+∞）时，不等式x²f（x）＞k（x-1）可变形为$k＜\frac{x（1+lnx）}{x-1}$
设$h（x）=\frac{x（1+lnx）}{x-1}$，（x＞1），则$h'（x）=\frac{x-lnx-2}{{{{（x-1）}^2}}}$
设φ（x）=x-lnx-2，（x＞1），则$φ'（x）=1-\frac{1}{x}$
因为x＞1时，$φ'（x）=\frac{x-1}{x}＞0$，所以φ（x）=x-lnx-2在（1，+∞）上单调递增，
又因为φ（3）=1-ln3＜0，φ（4）=2-ln4＞0
所以存在唯一的x₀∈（3，4），使得φ（x₀）=0，即lnx₀=x₀-2，
当x∈（1，x₀）时，φ（x）＜0，即h'（x₀）＜0，
当x∈（x₀，+∞）时，φ（x）＞0，即h'（x₀）＞0，
所以h（x）在（1，x₀）上单调递减，在（1，+∞）上单调递增，
故$h{（x）_{min}}=h（{x_0}）=\frac{{{x_0}（1+ln{x_0}）}}{{{x_0}-1}}=\frac{{{x_0}（1+{x_0}-2）}}{{{x_0}-1}}=\frac{{{x_0}（{x_0}-1）}}{{{x_0}-1}}={x_0}$，
因为$k＜{[{\frac{x（1+lnx）}{x-1}}]_{min}}={x_0}$，且x₀∈（3，4），
所以整数k的最大值为3．

点评 本题考查了函数的单调性、最值问题，考查导数的应用以及转化思想、数形结合思想，是一道中档题．