练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知是三角形的一个内角，且sin+cos=则方程xsin－ycos=1表示（    ）

    A  焦点在x轴上的双曲线         B       焦点在y轴上的双曲线

    C  焦点在x轴上的椭圆           D       焦点在y轴上的椭圆

    D 错因：学生不能由sin+cos=判断角为钝角。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知有关正三角形的一个结论：“在正三角形ABC中，若D是BC的中点，G是三角形ABC内切圆的圆心，则
    AG
    GD
    =2”．若把该结论推广到正四面体（所有棱长均相等的三棱锥），则有结论：“在正四面体ABCD中，若M是正三角形BCD的中心，O是在正四面体ABCD内切球的球心，则
    AO
    OM
    =
    3
    3
    ”．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆的内接三角形有一个顶点在短轴的顶点处，其重心是椭圆的一个焦点，求该椭圆离心率e的取值范围（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•宁波二模）三个顶点均在椭圆上的三角形称为椭圆的内接三角形．已知点A是椭圆的一个短轴端点，如果以A为直角顶点的椭圆内接等腰直角三角形有且仅有三个，则椭圆的离心率的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年湖北省高一理科实验班预录模拟数学试卷（解析版） 题型：解答题

    如图，已知锐角△ABC的面积为1，正方形DEFG是△ABC的一个内接三角形，

    DG∥BC，求正方形DEFG面积的最大值．

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年江苏省徐州市高二（下）期末数学试卷（文科）（解析版） 题型：填空题

    已知有关正三角形的一个结论：“在正三角形ABC中，若D是BC的中点，G是三角形ABC内切圆的圆心，则=2”．若把该结论推广到正四面体（所有棱长均相等的三棱锥），则有结论：“在正四面体ABCD中，若M是正三角形BCD的中心，O是在正四面体ABCD内切球的球心，则=    ”．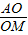

    查看答案和解析>>

    同步练习册答案