练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    抛掷红、蓝两颗骰子，设事件A为“蓝色骰子的点数为3或6”，事件B为“两颗骰子的点数之和大于8”．
    (1)求P(A)，P(B)，P(AB)；
    (2)当已知蓝色骰子的点数为3或6时，求两颗骰子的点数之和大于8的概率．

    (1)         (2)

    解析解:(1)①P(A)＝＝.
    ②∵两个骰子的点数之和共有36个等可能的结果，点数之和大于8的结果共有10个．
    ∴P(B)＝＝.
    ③当蓝色骰子的点数为3或6时，两颗骰子的点数之和大于8的结果有5个，故P(AB)＝.
    (2)由(1)知P(B|A)＝＝＝.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某高校在2012年自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)，第3组[85，90)，第4组[90，95)，第5组[95，100]得到的频率分布直方图如图所示．

    (1)分别求第3，4，5组的频率；
    (2)若该校决定在笔试成绩较高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，
    (ⅰ)已知学生甲和学生乙的成绩均在第三组，求学生甲和学生乙恰有一人进入第二轮面试的概率；
    (ⅱ)学校决定在这已抽取到的6名学生中随机抽取2名学生接受考官L的面试，设第4组中有名学生被考官L面试，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某计算机程序每运行一次都随机出现一个五位的二进制数A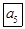＝，其中A的各位数中，a1＝1，ak(k＝2,3,4,5)出现0的概率为，出现1的概率为.记X＝a1＋a2＋a3＋a4＋a5，当程序运行一次时，
    (1)求X＝3的概率；
    (2)求X的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    A、B两个投资项目的利润率分别为随机变量X1和X2，根据市场分析，X1和X2的分布列分别为

    X1
    		5%
    		10%
    P
    		0.8
    		0.2
     
    X2
    		2%
    		8%
    		12%
    P
    		0.2
    		0.5
    		0.3
    (1)在A，B两个项目上各投资100万元，Y1和Y2分别表示投资项目A和B所获得的利润，求方差V(Y1)、V(Y2)；
    (2)将x(0≤x≤100)万元投资A项目，100－x万元投资B项目，f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和．求f(x)的最小值，并指出x为何值时，f(x)取到最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲、乙两人破译一密码，它们能破译的概率分别为和，试求：
    (1)两人都能破译的概率；
    (2)两人都不能破译的概率；
    (3)恰有一人能破译的概率；
    (4)至多有一人能破译的概率；
    (5)若要使破译的概率为99%，至少需要多少乙这样的人？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某校组织一次冬令营活动，有8名同学参加，其中有5名男同学，3名女同学，为了活动的需要，要从这8名同学中随机抽取3名同学去执行一项特殊任务，记其中有X名男同学．
    (1)求X的分布列；
    (2)求去执行任务的同学中有男有女的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某篮球运动员在最近几场大赛中罚球投篮的结果如下：

    投篮次数n
    		8
    		10
    		12
    		9
    		10
    		16
    进球次数m
    		6
    		8
    		9
    		7
    		7
    		12
    进球频率m/n
    		 
    		 
    		 
    		 
    		 
    		 
    (1)计算表中进球的频率；
    (2)这位运动员投篮一次，进球的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是,,且各轮次通过与否相互独立.
    (1)设该选手参赛的轮次为ξ,求ξ的分布列.
    (2)对于(1)中的ξ,设“函数f(x)=3sinπ(x∈R)是偶函数”为事件D,求事件D发生的概率.

    查看答案和解析>>

    同步练习册答案