
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点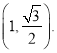
(1)求E的方程;
(2)若直线![]() 与E相交于
与E相交于![]() 两点,且
两点,且![]() 与
与![]() (
(![]() 为坐标原点)的斜率之和为2,求点
为坐标原点)的斜率之和为2,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0, ![]() ),以A,B为焦点且过点D的双曲线的离心率为e1 , 以C,D为焦点且过点A的椭圆的离心率为e2 , 则( )
),以A,B为焦点且过点D的双曲线的离心率为e1 , 以C,D为焦点且过点A的椭圆的离心率为e2 , 则( ) 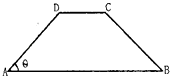
A.随着角度θ的增大,e1增大,e1e2为定值
B.随着角度θ的增大,e1减小,e1e2为定值
C.随着角度θ的增大,e1增大,e1e2也增大
D.随着角度θ的增大,e1减小,e1e2也减小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+y2=9内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程; (写一般式)
(2)当直线l的倾斜角为45°时,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为
,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为 ![]() +1 (Ⅰ)求椭圆C的方程;
+1 (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线L的斜率为k,且过左焦点F1 , 与椭圆C相交于P、Q两点,若△PQF2的面积为 ![]() ,试求k的值及直线L的方程.
,试求k的值及直线L的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组中的两个函数是同一函数的为( )
(1)f(x)=1,g(x)=x0
(2)f(x)= ![]() ,g(x)=
,g(x)= ![]()
(3)f(x)=lnxx , g(x)=elnx
(4)f(x)= ![]() ,g(x)=
,g(x)= ![]() .
.
A.(1)
B.(2)
C.(3)
D.(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)定义域内的任意x1 , x2(x1≠x2),有以下结论:
①f(0)=1;
②f(1)=0
③f(x1+x2)=f(x1)f(x2)
④f(x1x2)=f(x1)+f(x2)
⑤f( ![]() )<
)< ![]()
⑥f( ![]() )>
)> ![]()
当f(x)=2x时,则上述结论中成立的是(填入你认为正确的所有结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,函数f(x)= ![]() (a﹣x﹣ax),g(x)=﹣ax+2.
(a﹣x﹣ax),g(x)=﹣ax+2.
(1)指出f(x)的单调性(不要求证明);
(2)若有g(2)+f(2)=3,求g(﹣2)+f(﹣2)的值;
(3)若h(x)=f(x)+g(x)﹣2,求使不等式h(x2+tx)+h(4﹣x)<0恒成立的t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几年来,网上购物风靡,快递业迅猛发展,某市的快递业务主要由两家快递公司承接,即圆通公司与申通公司:“快递员”的工资是“底薪+送件提成”:这两家公司对“快递员”的日工资方案为:圆通公司规定快递员每天底薪为70元,每送件一次提成1元;申通公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成10元,假设同一公司的快递员每天送件数相同,现从这两家公司各随机抽取一名快递员并记录其100天的送件数,得到如下条形图:
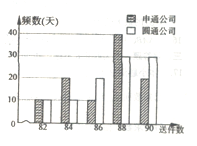
(1)求申通公司的快递员一日工资![]() (单位:元)与送件数
(单位:元)与送件数![]() 的函数关系;
的函数关系;
(2)若将频率视为概率,回答下列问题:
①记圆通公司的“快递员”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小王想到这两家公司中的一家应聘“快递员”的工作,如果仅从日收入的角度考虑,请你利用所学过的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com