
【题目】已知函数![]() 图象上点
图象上点![]() 处的切线方程与直线
处的切线方程与直线![]() 平行(其中
平行(其中![]() ),
),![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求函数![]() 在
在![]() (
(![]() )上的最小值;
)上的最小值;
(Ⅲ)对一切![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)  ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】试题分析:(I)根据切线方程与直线![]() 平行得到切线的斜率为2,即可得到
平行得到切线的斜率为2,即可得到![]() ,求出函数的导函数把
,求出函数的导函数把![]() 代入即可求出
代入即可求出![]() 的值得到函数的解析式;(II)令
的值得到函数的解析式;(II)令![]() 求出
求出![]() 的值为
的值为![]() ,由函数定义域
,由函数定义域![]() ,所以在
,所以在![]() 和
和![]() 上讨论函数的增减性,分两种情况:当
上讨论函数的增减性,分两种情况:当![]() 属于
属于![]() 得到函数的最小值为
得到函数的最小值为![]() ;当
;当![]() 时,根据函数为单调增得到函数的最小值为
时,根据函数为单调增得到函数的最小值为![]() ,求出值即可;(III)把
,求出值即可;(III)把![]() 的解析式代入不等式
的解析式代入不等式![]() 中解出
中解出![]() ,然后令
,然后令![]() ,求出
,求出![]() 时
时![]() 的值,然后在定义域
的值,然后在定义域![]() 上分区间讨论函数的增减性,求出
上分区间讨论函数的增减性,求出![]() 的最大值,
的最大值, ![]() 要大于等于
要大于等于![]() 的最大值即为不等数恒成立,即可求出
的最大值即为不等数恒成立,即可求出![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)由点![]() 处的切线方程为直线
处的切线方程为直线![]() 平行,
平行,
得该切线斜率为2,即![]() .
.
又![]() ,令
,令![]() ,
, ![]() ,所以
,所以![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,显然
,显然![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以函数![]() 在
在![]() 上单调递减.当
上单调递减.当![]() 时,
时, ![]() ,
,
所以函数![]() 在
在![]() 上单调递增.
上单调递增.
①![]() 时,
时, ![]()
![]() ;
;
②![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
因此![]()
![]() ;
;
所以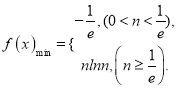
(Ⅲ)对一切![]() ,
, ![]() 恒成立,
恒成立,
又![]() ,
, ![]() ,
,
即![]() .
.
设![]() ,
, ![]() .
.
则![]()
![]()
![]() ,
,
由![]() 得
得![]() 或
或![]() ,
, ![]() ,
, ![]() ,
, ![]() 单调递增,
单调递增,
![]() ,
, ![]() ,
, ![]() 单调递减,
单调递减, ![]() ,
, ![]() ,
, ![]() 单调递增,
单调递增,
![]() ,且
,且![]()
![]() ,
,
所以![]() .
.
因为对一切![]() ,
, ![]() 恒成立,
恒成立,
![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】给出四个命题
(1)若sin2A=sin2B,则△ABC为等腰三角形;
(2)若sinA=cosB,则△ABC为直角三角形;
(3)若sin2A+sin2B+sin2C<2,则△ABC为钝角三角形;
(4)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形.
以上正确命题的是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,焦点到短轴端点的距离为2,离心率为
轴上,焦点到短轴端点的距离为2,离心率为![]() .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点且
两点且![]() ,是否存在以原点
,是否存在以原点![]() 为圆心的定圆与直线
为圆心的定圆与直线![]() 相切?若存在求出定圆的方程;若不存在,请说明理由
相切?若存在求出定圆的方程;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个结论:
(1)如果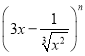 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中![]() 的系数是-21;
的系数是-21;
(2)用相关指数![]() 来刻画回归效果,
来刻画回归效果, ![]() 的值越大,说明模型的拟合效果越差;
的值越大,说明模型的拟合效果越差;
(3)若![]() 是
是![]() 上的奇函数,且满足
上的奇函数,且满足![]() ,则
,则![]() 的图象关于
的图象关于![]() 对称;
对称;
(4)一个篮球运动员投篮一次得3分的概率为![]() ,得2分的概率为
,得2分的概率为![]() ,不得分的概率为
,不得分的概率为![]() ,且
,且![]() ,已知他投篮一次得分的数学期望为2,则
,已知他投篮一次得分的数学期望为2,则![]() 的最小值为
的最小值为![]() ;
;
其中正确结论的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos xsin 2x,下列结论中正确的是________(填入正确结论的序号).
①y=f(x)的图象关于点(2π,0)中心对称;
②y=f(x)的图象关于直线x=π对称;
③f(x)的最大值为![]() ;
;
④f(x)既是奇函数,又是周期函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍。设购进A掀电脑x台,这100台电脑的销售总利润为y元。
①求y与x的关系式;
②该商店购进A型、B型各多少台,才能使销售利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台。若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=![]() ,连结椭圆的四个顶点得到的菱形的面积为4.
,连结椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设直线l与椭圆相交于不同的两点A,B.已知点A的坐标为(-a,0).若|AB|=![]() ,求直线l的倾斜角.
,求直线l的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
已知函数![]() (
(![]() 为常数)的图像与
为常数)的图像与![]() 轴交于点
轴交于点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
(1)求![]() 的值及函数
的值及函数![]() 的极值;
的极值;
(2)证明:当![]() 时,
时,![]()
(3)证明:对任意给定的正数![]() ,总存在
,总存在![]() ,使得当
,使得当![]() 时,恒有
时,恒有![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com