
【题目】有120粒试验种子需要播种,现有两种方案:方案一:将120粒种子分种在40个坑内,每坑3粒;方案二:120粒种子分种在60个坑内,每坑2粒 如果每粒种子发芽的概率为0.5,并且,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种(每个坑至多补种一次,且第二次补种的种子颗粒同第一次).假定每个坑第一次播种需要2元,补种1个坑需1元;每个成活的坑可收货100粒试验种子,每粒试验种子收益1元.
(1)用![]() 表示播种费用,分别求出两种方案的
表示播种费用,分别求出两种方案的![]() 的数学期望;
的数学期望;
(2)用![]() 表示收益,分别求出两种方案的收益
表示收益,分别求出两种方案的收益![]() 的数学期望;
的数学期望;
(3)如果在某块试验田对该种子进行试验,你认为应该选择哪种方案?
【答案】(1)答案见解析;(2)答案见解析;(3)方案二.
【解析】分析:(1)先确定播种费用随机变量,再计算对应概率,利用数学期望公式求期望,(2) 先确定收益随机变量,再计算对应概率,利用数学期望公式求期望,(3)根据纯利润的大小确定选择方案.
详解:
(1)方案一:用![]() 表示一个坑播种的费用,则
表示一个坑播种的费用,则![]() 可取2,3.
可取2,3.
| 2 | 3 |
|
|
|
∴ ![]() .
.
∴ ![]() 元.
元.
方案二:用![]() 表示一个坑播种的费用,则
表示一个坑播种的费用,则![]() 可取2,3.
可取2,3.
| 2 | 3 |
|
|
|
∴ ![]() .
.
∴ ![]() 元.
元.
(2)方案一:用![]() 表示一个坑的收益,则
表示一个坑的收益,则![]() 可取0,100.
可取0,100.
| 0 | 100 |
|
|
|
∴ ![]() .
.
∴ ![]() 元.
元.
方案二:用![]() 表示一个坑的收益,则
表示一个坑的收益,则![]() 可取0,100.
可取0,100.
| 0 | 100 |
|
|
|
∴ ![]() .
.
∴ ![]() 元.
元.
(3)方案二所需的播种费用比方案一多50元,但是收益比方案一多1687.5元,故应选择方案二.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
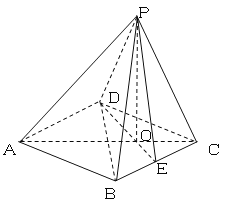
【题目】如图,已知四棱锥P-ABCD的底面是边长为2的菱形,∠BCD=60°,点E是BC边
的中点,AC,DE交于点O,![]() ,且PO⊥平面ABCD.
,且PO⊥平面ABCD.
(1)求证:PD⊥BC;
(2)在线段AP上找一点F,使得BF∥平面PDE,并求此时四面体PDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 同时满足:⑴对于定义域上的任意
同时满足:⑴对于定义域上的任意![]() ,恒有
,恒有![]() ; ⑵对于定义域上的任意
; ⑵对于定义域上的任意![]() ,当
,当![]() 时,恒有
时,恒有![]() ,则称函数
,则称函数![]() 为“理想函数”.给出下列四个函数中: ①
为“理想函数”.给出下列四个函数中: ①![]() ,②
,②![]() , ③
, ③![]() ,④
,④ ,能被称为“理想函数”的有_____________(填相应的序号).
,能被称为“理想函数”的有_____________(填相应的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如下图).由图中数据可知a=________,估计该小学学生身高的中位数为______

查看答案和解析>>
科目:高中数学 来源: 题型:
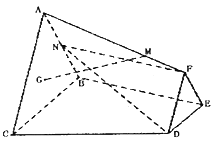
【题目】如图,已知![]() 与
与![]() 分别是边长为1与2的正三角形,
分别是边长为1与2的正三角形,![]() ,四边形
,四边形![]() 为直角梯形,且
为直角梯形,且![]() ,
,![]() ,点
,点![]() 为
为![]() 的重心,
的重心,![]() 为
为![]() 中点,
中点,![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的三等分点.
的三等分点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,试求异面直线
,试求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,底面
,底面![]() 是梯形,AB∥CD,
是梯形,AB∥CD,![]() ,AB=PD=4,CD=2,
,AB=PD=4,CD=2,![]() ,M为CD的中点,N为PB上一点,且
,M为CD的中点,N为PB上一点,且![]() .
.
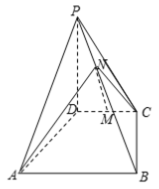
(1)若![]() MN∥平面PAD;
MN∥平面PAD;
(2)若直线AN与平面PBC所成角的正弦值为![]() ,求异面直线AD与直线CN所成角的余弦值.
,求异面直线AD与直线CN所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com