
| A. | 2026 | B. | 2057 | C. | 2073 | D. | 2074 |
分析 利用对数的运算性质可知a1•a2•a3•…•ak=$\frac{lg(k+2)}{lg2}$,进而计算可得结论.
解答 解:∵an=logn+1(n+2)(n∈N*),
∴a1•a2•a3•…•ak=$\frac{lg3}{lg2}$•$\frac{lg4}{lg3}$•…•$\frac{lg(k+1)}{lgk}$•$\frac{lg(k+2)}{lg(k+1)}$=$\frac{lg(k+2)}{lg2}$,
∴k+2=2t(t≥2,t∈N*),
于是区间[1,2016]内的所有企盼数的和为(22-2)+(23-2)+…+(210-2)=$\frac{{2}^{2}(1-{2}^{9})}{1-2}$-2×9=2026,
故选:A.
点评 本题考查数列的通项,考查运算求解能力,利用对数的性质是解决本题的关键,注意解题方法的积累,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [1,7] | C. | [7,9] | D. | [9,21] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
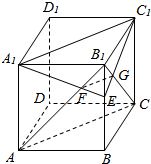 如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.
如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{12}$ | B. | $\frac{10}{11}$ | C. | $\frac{9}{10}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com