练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数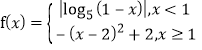，则方程（）的实数根个数不可能为（ ）

    A. 5个 B. 6个 C. 7个 D. 8个

    【答案】A

    【解析】

    以f（x）＝1的特殊情形为突破口，解出x＝1或3或或﹣4，将x+﹣2看作整体，利用换元的思想方法进一步讨论．

    ∵函数，

    即f（x）＝，

    因为当f（x）＝1时，x＝1或3或或﹣4，

    则当a＝1时，x+﹣2＝1或3或或﹣4，

    又因为 x+﹣2≥0或x+﹣2≤﹣4，

    所以，当x+﹣2＝﹣4时只有一个x＝﹣2与之对应．

    其它情况都有2个x值与之对应，故此时所求的方程有7个根，

    当1＜a＜2时，y＝f（x）与y＝a有4个交点，故有8个根；

    当a＝2时，y＝f（x）与y＝a有3个交点，故有6个根；

    综上：不可能有5个根，

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校计划面向高二年级文科学生开设社会科学类和自然退坡在校本选修课程，某文科班有50名学生，对该班选课情况进行统计可知：女生占班级人数的60％，选社会科学类的人数占班级人数的70％，男生有10人选自然科学类．

    （1）根据题意完成以下列联表：

    选择自然科学类

    选择社会科学类

    合计

    男生

    女生

    （2）判断是否有99％的把握认为科类的选择与性别有关？

    附：，其中．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）当时，求在点处的切线方程；

    （Ⅱ）若，求函数的单调区间；

    （Ⅲ）若对任意的，在上恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）指出函数的基本性质：定义域，奇偶性，单调性，值域（结论不需证明），并作出函数的图象；

    （2）若关于的不等式恒成立，求实数的取值范围；

    （3）若关于的方程恰有个不同的实数解，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在梯形中，∥，，，，且，又平面，.

    求：（1）二面角的大小（用反三角函数表示）；

    （2）点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在等差数列中，，.

    （1）求数列的通项公式；

    （2）对任意，将数列中落入区间内的项的个数记为，记数列的前项和为，求使得的最小整数；

    （3）若 ，使不等式成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量，记．

    （1）若，求的值；

    （2）在锐角中，角的对边分别是，且满足，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝4cos ωx·sin＋a(ω>0)图象上最高点的纵坐标为2，且图象上相邻两个最高点的距离为π.

    (1)求a和ω的值；

    (2)求函数f(x)在[0，π]上的单调递减区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 .

    (1)若，求的最小值；

    (2)若,求的单调区间；

    (3)试比较与的大小,并证明你的结论.

    查看答案和解析>>

    同步练习册答案