
【题目】已知椭圆![]() 过点
过点![]() ,右顶点为点
,右顶点为点![]() .
.
(1)若直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() 两点(
两点(![]() 不是左、右顶点),且
不是左、右顶点),且![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(2)![]() 是椭圆
是椭圆![]() 的两个动点,若直线
的两个动点,若直线![]() 的斜率与
的斜率与![]() 的斜率互为相反数,试判断直线EF的斜率是否为定值?如果是,求出定值;反之,请说明理由.
的斜率互为相反数,试判断直线EF的斜率是否为定值?如果是,求出定值;反之,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1) 设![]() (x1,y1),
(x1,y1),![]() (x2,y2),联立方程组根据根与系数的关系,利用
(x2,y2),联立方程组根据根与系数的关系,利用![]() ,得到
,得到![]() ,即可得出;
,即可得出;
(2) 设点![]() 坐标分别为
坐标分别为![]() ,设直线EF的方程为
,设直线EF的方程为![]() ,联立方程得到
,联立方程得到![]() ,利用韦达定理表示
,利用韦达定理表示![]() ,即可得到结果.
,即可得到结果.
(1)设点![]() 坐标分别为
坐标分别为![]() ,点
,点![]() 坐标为
坐标为![]() ,因为
,因为![]() ,则
,则
![]() ,又
,又![]() ,代入整理得
,代入整理得
![]() , (*)
, (*)
由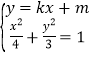 得
得![]() ,当
,当![]() 时,方程两根为
时,方程两根为![]() ,则有
,则有
![]() ,代入(*)得
,代入(*)得![]() ,
,
所以![]() 或
或![]() ,
,
当![]() 时,直线方程为
时,直线方程为![]() ,恒过点
,恒过点![]() ,不符合题意,舍去;
,不符合题意,舍去;
当![]() 时,直线方程为
时,直线方程为![]() ,恒过点
,恒过点![]() ,该点在椭圆内,则
,该点在椭圆内,则![]() 恒成立,
恒成立,
所以,直线![]() 过定点
过定点![]() .
.
(2)设点![]() 坐标分别为
坐标分别为![]() ,直线
,直线![]() 、EF的斜率显然存在,
、EF的斜率显然存在,
所以![]() ,设直线EF的方程为
,设直线EF的方程为![]() ,同(1)
,同(1)
由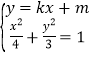 得
得![]() ,(#)
,(#)
当![]() 时,方程两根为
时,方程两根为![]() ,则有
,则有![]() ,①
,①
因为直线![]() 的斜率与
的斜率与![]() 的斜率互为相反数,则
的斜率互为相反数,则
![]() ,又
,又![]() ,代入整理得
,代入整理得
![]() , ②
, ②
①代入②,化简得![]() ,即
,即![]()
所以![]() 或
或![]() ,
,
当![]() 时,直线
时,直线![]() 方程为
方程为![]() ,恒过点
,恒过点![]() ,不符合题意,舍去;
,不符合题意,舍去;
当![]() 时,方程(#)即
时,方程(#)即![]() ,则
,则![]() 时,
时,![]() ,
,
所以当![]() 且
且![]() 时,
时,![]() 恒成立,
恒成立,
所以,直线EF的斜率为定值![]() .
.


科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosx,sinx),
=(cosx,sinx), ![]() =(3,﹣
=(3,﹣ ![]() ),x∈[0,π].
),x∈[0,π].
(Ⅰ)若 ![]() ∥
∥ ![]() ,求x的值;
,求x的值;
(Ⅱ)记f(x)= ![]() ,求f(x)的最大值和最小值以及对应的x的值.
,求f(x)的最大值和最小值以及对应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,空间四边形ABCD的两条对棱AC,BD互相垂直,AC,BD的长分别为8和2,则平行四边形两条对棱的截面四边形EFGH在平移过程中,面积的最大值是_______________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.
(Ⅰ)M为曲线C1上的动点,点P在线段OM上,且满足|OM||OP|=16,求点P的轨迹C2的直角坐标方程;
(Ⅱ)设点A的极坐标为(2, ![]() ),点B在曲线C2上,求△OAB面积的最大值.
),点B在曲线C2上,求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:
①“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②“![]() ”是“一元二次不等式
”是“一元二次不等式![]() 的解集为R”的充要条件;
的解集为R”的充要条件;
③“![]() ”是“直线
”是“直线![]() 平行于直线
平行于直线![]() ”的充分不必要条件;
”的充分不必要条件;
④“![]() ”是“
”是“![]() ”的必要不充分条件.
”的必要不充分条件.
其中真命题的序号为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com