
【题目】如图,在多面体![]() 中,平面
中,平面![]() 与平面
与平面![]() 垂直,
垂直,![]() 是正方形,在直角梯形
是正方形,在直角梯形![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
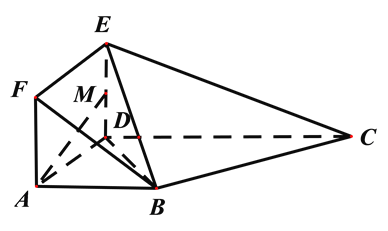
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】学校将5个参加知识竞赛的名额全部分配给高二年级的4个班级,其中甲班级至少分配2个名额,其它班级可以不分配名额或分配多个名额,则不同的分配方案共有( )
A.30种 B.26种 C.24种 D.20种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面五边形![]() 是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,
是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,![]() ,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
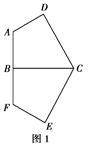
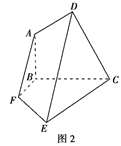
(1)证明:AF∥平面DEC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在整数集![]() 中,被4除所得余数为
中,被4除所得余数为![]() 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为![]() ,则下列结论正确的为 .
,则下列结论正确的为 .
①2014![]() ;
;
②-1![]() ;
;
③![]() ;
;
④命题“整数![]() 满足
满足![]() ,则
,则![]() ”的原命题与逆命题都正确;
”的原命题与逆命题都正确;
⑤“整数![]() 属于同一类”的充要条件是“
属于同一类”的充要条件是“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.”某市交警在该市一交通岗前设点对过往的车辆进行抽查,经过一晚的抽查,共查出酒后驾车者60名,图甲是用酒精测试仪对这60 名酒后驾车者血液中酒精浓度进行检测后依所得结果画出的频率分布直方图.
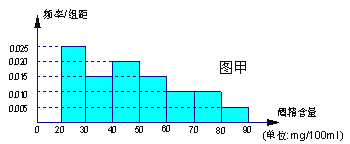
(1)统计方法中,同一组数据常用该组区间的中点值作为代表,图乙的程序框图是对这60名酒后驾车者血液的酒精浓度做进一步的统计,求出图乙输出的S的值,并说明S的统计意义;(图乙中数据![]() 与
与![]() 分别表示图甲中各组的组中值及频率)
分别表示图甲中各组的组中值及频率)

(2)本次行动中,吴、李两位先生都被酒精测试仪测得酒精浓度属于70~90![]() 的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90
的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90![]() 范围的酒后驾车者中随机抽出2人抽血检验,设
范围的酒后驾车者中随机抽出2人抽血检验,设![]() 为吴、李两位先生被抽中的人数,求
为吴、李两位先生被抽中的人数,求![]() 的分布列,并求吴、李两位先生至少有1人被抽中的概率.
的分布列,并求吴、李两位先生至少有1人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
组别 | 候车时间 | 人数 |
一 |
| 2 |
二 |
| 6 |
三 |
| 4 |
四 |
| 2 |
五 |
| 1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 在它的某一个周期内的单调减区间是
在它的某一个周期内的单调减区间是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)将![]() 的图象先向右平移
的图象先向右平移![]() 个单位,再将图象上所有点的横坐标变为原来的
个单位,再将图象上所有点的横坐标变为原来的![]() 倍(纵坐标不变),所得到的图象对应的函数记为
倍(纵坐标不变),所得到的图象对应的函数记为![]() ,若对于任意的
,若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数![]() 的图像过定点
的图像过定点![]() ;
;
②已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() ,则
,则![]() 的解析式为
的解析式为![]() ;
;
③函数![]() 的图像可由函数
的图像可由函数![]() 图像向右平移一个单位得到;
图像向右平移一个单位得到;
④函数![]() 图像上的点到
图像上的点到![]() 距离的最小值是
距离的最小值是![]() .
.
其中所有正确命题的序号是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com