
【题目】已知曲线C的参数方程为![]() (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)直线l与曲线C是否有公共点?并说明理由;
(2)若直线l与两坐标轴的交点为A,B,点P是曲线C上的一点,求△PAB的面积的最大值.
【答案】(1)没有交点,理由见详解;(2)3![]() .
.
【解析】
(1)将曲线![]() 的参数方程化为普通方程,将直线
的参数方程化为普通方程,将直线![]() 的极坐标方程化为直角方程,联立方程组,根据
的极坐标方程化为直角方程,联立方程组,根据![]() 的情况,求得两曲线的相交情况;
的情况,求得两曲线的相交情况;
(2)由(1)中所求,容易得点![]() 的坐标,设点
的坐标,设点![]() 坐标为(3cosθ,sinθ),再将问题转化为三角函数值域的问题即可求得.
坐标为(3cosθ,sinθ),再将问题转化为三角函数值域的问题即可求得.
(1)曲线C的参数方程为![]() (φ为参数),
(φ为参数),
转换为直角坐标方程为![]() .
.
直线l的极坐标方程为![]() ,
,
整理得![]() ,
,
转换为直角坐标方程为x﹣y﹣6=0,
联立方程组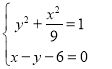
消去![]() ,可得10y2+12y+27=0,
,可得10y2+12y+27=0,
由于△=122﹣4×10×27<0,所以直线与椭圆没有交点.
(2)直线的直角坐标方程为x﹣y﹣6=0,
与x轴的交点A(6,0)与y轴的交点坐标为B(0,6),
所以|AB|![]() ,
,
设椭圆上点P的坐标为(3cosθ,sinθ),
所以点P到直线l的距离d
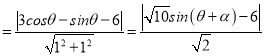 ,
,
当![]() 时,
时,![]() ,
,
则![]() 3
3![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() x3+ax2+bx,且f′(﹣1)=0.
x3+ax2+bx,且f′(﹣1)=0.
(1)试用含a的代数式表示b;
(2)求f(x)的单调区间;
(3)令a=﹣1,设函数f(x)在x1、x2(x1<x2)处取得极值,记点M(x1,f(x1)),N(x2,f(x2)).证明:线段MN与曲线f(x)存在异于M,N的公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() ),
),![]() 和
和![]() 是函数
是函数![]() 的图象与
的图象与![]() 轴的2个相邻交点的横坐标,且当
轴的2个相邻交点的横坐标,且当![]() 时,
时,![]() 取得最大值2.
取得最大值2.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)将函数![]() 的图象上的每一点的横坐标变为原来的
的图象上的每一点的横坐标变为原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象,再将函数
的图象,再将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,椭圆
轴的正半轴为极轴建立极坐标系,椭圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程(写成一般式)和椭圆
的普通方程(写成一般式)和椭圆![]() 的直角坐标方程(写成标准方程);
的直角坐标方程(写成标准方程);
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本小题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别![]()
![]() ,假设
,假设![]() 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(1)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为![]() ,其中
,其中![]() 是
是![]() 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目![]() 的分布列和均值(数字期望)
的分布列和均值(数字期望)![]() ;
;
(3)假定![]() ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com