
����Ŀ�����ں���f1��x����f2��x����h��x�����������ʵ��a��bʹ��h��x��=af1��x��+bf2��x������ô��h��x��Ϊf1��x����f2��x���ĺ�г������
��1����֪����f1��x��=x��1��f2��x��=3x+1��h��x��=2x+2�����ж�h��x���Ƿ�Ϊf1��x����f2��x���ĺ�г��������˵�����ɣ�
��2����֪h��x��Ϊ����f1��x��=log3x��f2��x��=log ![]() x�ĺ�г����������a=2��b=1��������h��9x��+th��3x��=0��x��[3��9]���н⣬��ʵ��t��ȡֵ��Χ��
x�ĺ�г����������a=2��b=1��������h��9x��+th��3x��=0��x��[3��9]���н⣬��ʵ��t��ȡֵ��Χ��
���𰸡�
��1���⣺h��x����f1��x����f2��x���ĺ�г��������Ϊ����a=��1��b=1
ʹh��x��=��f1��x��+f2��x��
��h��x��=af1��x��+bf2��x������2x+2=a��x��1��+b��3x+1����
���� ![]() ��
�� ![]()
����h��x����f1��x����f2��x���ĺ�г����
��2���⣺�ⷨһ�������⣬�ɷ��� ![]() ��x��[3��9]���н⣬��log3��9x��+tlog3��3x��=0��x��[3��9]���н⣬
��x��[3��9]���н⣬��log3��9x��+tlog3��3x��=0��x��[3��9]���н⣬
����ã�2+log3x+t��1+log3x��=0
��m=log3x��x��[3��9]����m��[1��2]���� ��1+m��t+��t+2��=0
ԭ�������ת������m�ķ��̣�1+t��m+��t+2��=0��m��[1��2]���н⣬
��g��m��=��1+t��m+��t+2��
������ã�g��1��g��2����0����� ![]() ��
��
���ϣ� ![]()
�ⷨ����log3��9x��+tlog3��3x��=0������ã�2+log3x+t��1+log3x��=0
��Ϊx��[3��9]�����ԣ�1+log3x����[2��3]��
ԭʽ��ת��Ϊ���� ![]() ��x��[3��9]�������н�
��x��[3��9]�������н�
������ ![]() ��x��[3��9]��ֵ��
��x��[3��9]��ֵ��
�� ![]() ����Ϊ 2��1+log3x��3
����Ϊ 2��1+log3x��3
�ɷ������������ʿɵã�����g��x����ֵ��Ϊ ![]()
����ʵ��t��ȡֵ��Χ ![]()
����������1��h��x����f1��x����f2��x���ĺ�г����������a=��1��b=1����h��x��=af1��x��+bf2��x���������¶����жϼ��ɣ���2���ⷨһ������ ![]() ��x��[3��9]���н⣬��log3��9x��+tlog3��3x��=0��x��[3��9]���н⣬��m=log3x��x��[3��9]����m��[1��2]��ԭ�������ת������m�ķ��̣�1+t��m+��t+2��=0��m��[1��2]���н⣬��g��m��=��1+t��m+��t+2��ͨ��g��1��g��2����0����⼴�ɣ���2���ⷨ����log3��9x��+tlog3��3x��=0������ã�2+log3x+t��1+log3x��=0��ԭʽ��ת��Ϊ����
��x��[3��9]���н⣬��log3��9x��+tlog3��3x��=0��x��[3��9]���н⣬��m=log3x��x��[3��9]����m��[1��2]��ԭ�������ת������m�ķ��̣�1+t��m+��t+2��=0��m��[1��2]���н⣬��g��m��=��1+t��m+��t+2��ͨ��g��1��g��2����0����⼴�ɣ���2���ⷨ����log3��9x��+tlog3��3x��=0������ã�2+log3x+t��1+log3x��=0��ԭʽ��ת��Ϊ���� ![]() ��x��[3��9]�������н⣬������
��x��[3��9]�������н⣬������ ![]() ��x��[3��9]��ֵ��ͨ�����볣��������⼴�ɣ�
��x��[3��9]��ֵ��ͨ�����볣��������⼴�ɣ�
�����㾫����������Ҫ�����˺�����ֵ�����֪ʶ�㣬��Ҫ���պ���ֵ�������䷽��(���λ��Ĵ�)���ڡ��б�ʽ�������۷����������ܻ�Ԫ�����ݲ���ʽ���������ĵ����Է�������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ��Ϊ![]() ��Բ����
��Բ����![]() ��
��![]() ����Բ����ֱ��
����Բ����ֱ��![]() ��
�� ![]() ��.
��.
��1����Բ��Ϊ![]() ��Բ�ı����̣�
��Բ�ı����̣�
��2������ ![]() ��Բ�����ߣ������߷���.
��Բ�����ߣ������߷���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������M={x|��2��x��2��N=y|0��y��2}�����������ĸ�ͼ�Σ������ܱ�ʾ��MΪ������NΪֵ��ĺ�����ϵ�� �� 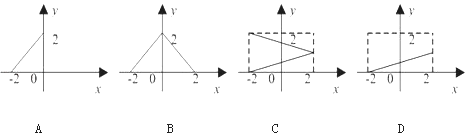
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=f��x����R��Ϊ�溯������x��0ʱ��f��x��=3x2��9����f����2��=
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������ס�������������Ʒ��ÿ����������ֱ�Ϊ3��Ԫ��2��Ԫ���ס��Ҳ�Ʒ����Ҫ��![]() �����豸�ϼӹ�����ÿ̨
�����豸�ϼӹ�����ÿ̨![]() �ϼӹ�1�������蹤ʱ�ֱ���1
�ϼӹ�1�������蹤ʱ�ֱ���1![]() ��2
��2![]() ���ӹ�1�������蹤ʱ�ֱ�Ϊ2
���ӹ�1�������蹤ʱ�ֱ�Ϊ2![]() ��1
��1![]() ��
�� ![]() �����豸ÿ����Чʹ��̨ʱ���ֱ�Ϊ400
�����豸ÿ����Чʹ��̨ʱ���ֱ�Ϊ400![]() ��500
��500![]() ����ΰ���������ʹ�������
����ΰ���������ʹ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
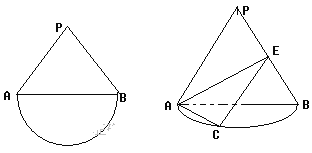
����Ŀ����ͼ��һ���߳�Ϊ![]() ���������κͰ�Բ��ɵ�ͼ�Σ��ְ�
���������κͰ�Բ��ɵ�ͼ�Σ��ְ�![]() ��ֱ��AB����ʹ����Բ����ƽ�洹ֱ����֪��C�ǰ�Բ��һ�����ȷֵ㣨�����һ�㣩����E���߶�PB�ϵĵ㣬��1������E��PB���е�ʱ����Բ������һ��Q��ʹ��
��ֱ��AB����ʹ����Բ����ƽ�洹ֱ����֪��C�ǰ�Բ��һ�����ȷֵ㣨�����һ�㣩����E���߶�PB�ϵĵ㣬��1������E��PB���е�ʱ����Բ������һ��Q��ʹ��![]() ƽ��
ƽ��![]() ����2���������
����2���������![]() ������ֵΪ
������ֵΪ![]() ʱ����BE�ij���
ʱ����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���׳������������������۾���õ������й��������۵�ͳ�ƹ��ɣ�ÿ������Ʒx����̨�������ܳɱ�ΪG��x������Ԫ�������й̶��ɱ�Ϊ2.8��Ԫ������ÿ����1��̨�������ɱ�Ϊ1��Ԫ���ܳɱ�=�̶��ɱ�+�����ɱ�������������R��x������Ԫ������R��x��= ![]() ���ٶ��ò�Ʒ����ƽ�⣨�������IJ�Ʒ��������������������ͳ�ƹ��ɣ�������������⣺
���ٶ��ò�Ʒ����ƽ�⣨�������IJ�Ʒ��������������������ͳ�ƹ��ɣ�������������⣺
��1��д��������y=f��x���Ľ���ʽ������=�������멁�ܳɱ�����
��2��Ҫʹ�׳���ӯ���������x�ķ�Χ��
��3���׳���������̨��Ʒʱ����ʹӯ����ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Ϊ2����ԲW�� ![]() ��a��b��0�������ҽ���ֱ�ΪA1��A2���ϡ��¶���ֱ�ΪB1��B2����M��x0��y0��Ϊ��ԲW�ϲ����������ϵ�����һ�㣬������ֱ��MA1��MA2��MB1��MB2��б��֮��Ϊ
��a��b��0�������ҽ���ֱ�ΪA1��A2���ϡ��¶���ֱ�ΪB1��B2����M��x0��y0��Ϊ��ԲW�ϲ����������ϵ�����һ�㣬������ֱ��MA1��MA2��MB1��MB2��б��֮��Ϊ![]() ��
��
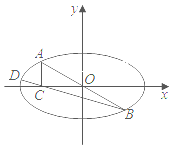
��1������ԲW�ı����̣�
��2����ͼ��ʾ����A��D����ԲW�����㣬��A���B����ԭ��Գƣ�AD��AB����C��x���ϣ���AC��x�ᴹֱ����֤��B��C��D���㹲�ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() �������߷���Ϊ
�������߷���Ϊ![]()
��������![]() �ĵ������䣻
�ĵ������䣻
������![]() ��������
Ϊ��������![]() ʱ��
ʱ�� ![]() ���������
���������![]() �����ֵ������
�����ֵ������![]() Ϊ
Ϊ![]() �ĵ���������
�ĵ���������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com