
【题目】已知数列![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(1)证明:数列![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)在数列![]() 中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(3)若![]() 且
且![]() ,
,![]() ,求证:使得
,求证:使得![]() ,
,![]() ,
,![]() 成等差数列的点列
成等差数列的点列![]() 在某一直线上.
在某一直线上.
【答案】(1)详见解析;(2)![]() ,
,![]() ,
,![]() 成等差数列;(3)详见解析.
成等差数列;(3)详见解析.
【解析】
试题(1)证明一个数列为等比或等差数列,一般都是从定义入手,本小题首先需要将已知条件![]() 变形为
变形为![]() ,由于
,由于![]() ,则
,则![]() (常数),然后根据等比数列的定义可知数列
(常数),然后根据等比数列的定义可知数列![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列,即
的等比数列,即![]()
![]() (
(![]() );
);
(2)本小题首先假设在数列![]() 中存在连续三项
中存在连续三项![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() )成等差数列,则
)成等差数列,则![]() ,代入通项公式可得
,代入通项公式可得![]() ,即
,即![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(3)本小题首先根据![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() ,于是可得
,于是可得![]() ,然后通过不定方程的分类讨论可得结论
,然后通过不定方程的分类讨论可得结论
试题解析:(1)将已知条件![]() 变形为
变形为![]()
由于![]() ,则
,则![]() (常数)
(常数)
即数列![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列
的等比数列
所以![]()
![]() ,即
,即![]()
![]() (
(![]() )
)
(2)假设在数列![]() 中存在连续三项成等差数列,
中存在连续三项成等差数列,
不妨设连续的三项依次为![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ),
),
由题意得,![]() ,
,
将![]() ,
,![]() ,
,![]() 代入上式得
代入上式得
![]()
化简得,![]() ,即
,即![]() ,得
,得![]() ,解得
,解得![]()
所以,存在满足条件的连续三项为![]() ,
,![]() ,
,![]() 成等差数列
成等差数列
(3)若![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]()
即![]() ,变形得
,变形得![]() 11分
11分
由于若![]() ,
,![]() 且
且![]() ,下面对
,下面对![]() 、
、![]() 进行讨论:
进行讨论:
① 若![]() ,
,![]() 均为偶数,则
均为偶数,则![]() ,解得
,解得![]() ,与
,与![]() 矛盾,舍去;
矛盾,舍去;
② 若![]() 为奇数,
为奇数,![]() 为偶数,则
为偶数,则![]() ,解得
,解得![]() ;
;
③ 若![]() 为偶数,
为偶数,![]() 为奇数,则
为奇数,则![]() ,解得
,解得![]() ,与
,与![]() 矛盾,舍去;
矛盾,舍去;
④ 若![]() ,
,![]() 均为奇数,则
均为奇数,则![]() ,解得
,解得![]() ,与
,与![]() 矛盾,舍去;
矛盾,舍去;
综上①②③④可知,只有当![]() 为奇数,
为奇数,![]() 为偶数时,
为偶数时,![]() ,
,![]() ,
,![]() 成等差数列,此时满足条
成等差数列,此时满足条
件点列![]() 落在直线
落在直线![]() (其中
(其中![]() 为正奇数)上
为正奇数)上


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,离心率
,离心率![]() ,长轴与短轴的长度之和为
,长轴与短轴的长度之和为![]() .
.

(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)在椭圆![]() 上任取点
上任取点![]() (与
(与![]() 两点不重合),直线
两点不重合),直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数![]() 是一种反映和评价空气质量的方法,
是一种反映和评价空气质量的方法,![]() 指数与空气质量对应如下表所示:
指数与空气质量对应如下表所示:

如图是某城市2018年12月全月的指![]() 数变化统计图.
数变化统计图.
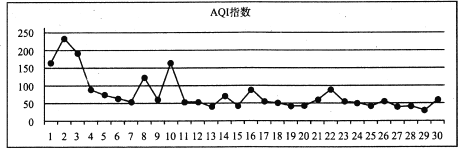
根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半月的空气质量
C. 从![]() 数据看,前半月的方差大于后半月的方差
数据看,前半月的方差大于后半月的方差
D. 从![]() 数据看,前半月的平均值小于后半月的平均值
数据看,前半月的平均值小于后半月的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x3﹣3ax2+1.
(1)若a=﹣1,求函数f(x)的单调区间;
(2)若函数f(x)有且只有2个不同的零点,求实数a的值;
(3)若函数y=|f(x)|在[0,1]上的最小值是0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 是圆
是圆![]() 与圆
与圆![]() 的公共弦
的公共弦![]() 所在直线方程,且圆
所在直线方程,且圆![]() 的圆心在直线
的圆心在直线![]() 上.
上.
(1)求公共弦![]() 的长度;
的长度;
(2)求圆![]() 的方程;
的方程;
(3)过点![]() 分别作直线
分别作直线![]() ,
,![]() ,交圆
,交圆![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四点,且
四点,且![]() ,求四边形
,求四边形![]() 面积的最大值与最小值.
面积的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是一门以不规则几何形态为研究对象的几何学.分形的外表结构极为复杂,但其内部却是有规律可寻的.一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.下面我们用分形的方法来得到一系列图形,如图1,线段![]() 的长度为a,在线段
的长度为a,在线段![]() 上取两个点
上取两个点![]() ,
,![]() ,使得
,使得![]() ,以
,以![]() 为一边在线段
为一边在线段![]() 的上方做一个正六边形,然后去掉线段
的上方做一个正六边形,然后去掉线段![]() ,得到图2中的图形;对图2中的最上方的线段
,得到图2中的图形;对图2中的最上方的线段![]() 作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:
作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:

记第![]() 个图形(图1为第1个图形)中的所有线段长的和为
个图形(图1为第1个图形)中的所有线段长的和为![]() ,现给出有关数列
,现给出有关数列![]() 的四个命题:
的四个命题:
①数列![]() 是等比数列;
是等比数列;
②数列![]() 是递增数列;
是递增数列;
③存在最小的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() ;
;
④存在最大的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() .
.
其中真命题的序号是________________(请写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制得到下面的散点图.
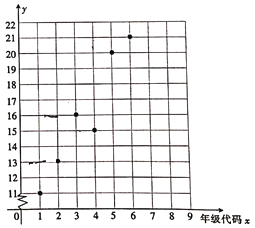
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
附注:参考数据:![]()
参考公式:相关系数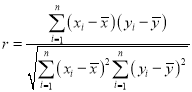 ,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为![]() =
=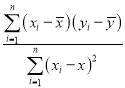 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,
轴上,![]() 为椭圆
为椭圆![]() 短轴的一个端点,
短轴的一个端点,![]() 为椭圆
为椭圆![]() 的右焦点,线段
的右焦点,线段![]() 的延长线与椭圆
的延长线与椭圆![]() 相交于点
相交于点![]() ,且
,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,若直线
为坐标原点,若直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时期的数学家祖暅提出了计算体积的祖暅原理:“幂势既同,则积不容异。”意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.已知曲线![]() ,直线
,直线![]() 为曲线
为曲线![]() 在点
在点![]() 处的切线.如图所示,阴影部分为曲线
处的切线.如图所示,阴影部分为曲线![]() 、直线
、直线![]() 以及
以及![]() 轴所围成的平面图形,记该平面图形绕
轴所围成的平面图形,记该平面图形绕![]() 轴旋转一周所得的几何体为
轴旋转一周所得的几何体为![]() .给出以下四个几何体:
.给出以下四个几何体:





① ② ③ ④
图①是底面直径和高均为![]() 的圆锥;
的圆锥;
图②是将底面直径和高均为![]() 的圆柱挖掉一个与圆柱同底等高的倒置圆锥得到的几何体;
的圆柱挖掉一个与圆柱同底等高的倒置圆锥得到的几何体;
图③是底面边长和高均为![]() 的正四棱锥;
的正四棱锥;
图④是将上底面直径为![]() ,下底面直径为
,下底面直径为![]() ,高为
,高为![]() 的圆台挖掉一个底面直径为
的圆台挖掉一个底面直径为![]() ,高为
,高为![]() 的倒置圆锥得到的几何体.
的倒置圆锥得到的几何体.
根据祖暅原理,以上四个几何体中与![]() 的体积相等的是( )
的体积相等的是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com