
(本小题满分12分)一个四棱锥的直观图和三视图如图所示: 

(1)求证: ⊥
⊥ ;
;
(2)求出这个几何体的体积。
(3)若在PC上有一点E,满足CE:EP=2:1,求证PA//平面BED。
(1)∵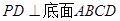 ,
,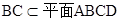
∴ 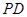 ⊥
⊥ , 在梯形
, 在梯形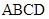 中,
中,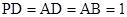 ,
,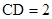
∴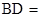
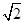 ,又可得
,又可得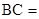
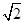 ,
,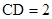 ,∴
,∴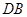 ⊥
⊥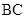 ,
,
又∵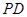
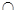
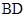
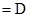 ,
,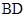 ,
,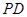
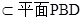 ∴
∴ ⊥面
⊥面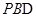 ,
,
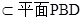
∴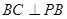
(2)4;(3)连结AC,设AC交BD于O点, 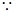 CD//AB,CD=2AB,
CD//AB,CD=2AB,
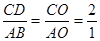
又
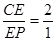
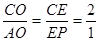 ,
, PA//EO,
PA//EO, PA//平面BED
PA//平面BED
解析试题分析:由三视图可知: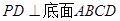 ,底面ABCD为直角梯形,,
,底面ABCD为直角梯形,,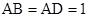 ,
,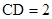 ,(1)∵
,(1)∵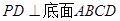 ,
,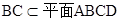
∴ 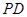 ⊥
⊥ , 在梯形
, 在梯形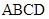 中,
中,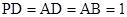 ,
,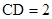
∴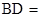
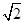 ,又可得
,又可得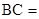
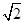 ,
,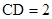 ,
,
∴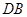 ⊥
⊥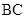 ,
,
又∵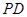
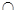
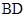
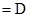 ,
,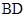 ,
,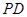
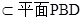
∴ ⊥面
⊥面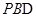 ,
,
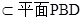
∴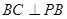
(2)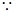 PD
PD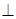 平面ABCD,
平面ABCD,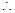 PD是这个四棱锥的高,又底面
PD是这个四棱锥的高,又底面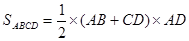
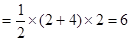 ,所以
,所以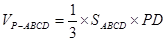
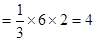
(3)连结AC,设AC交BD于O点, 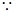 CD//AB ,CD=2AB,
CD//AB ,CD=2AB,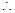
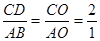
又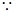
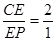
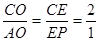 ,
,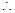 PA//EO,EO
PA//EO,EO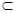 平面BED ,PA
平面BED ,PA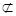 平面BE
平面BE 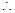 PA//平面BED
PA//平面BED
考点:本题考查了空间中的线面关系及体积的求法
点评:高考中常考查空间中平行关系与垂直关系的证明以及几何体体积的计算,这是高考的重点内容.证明的关键是熟练掌握并灵活运用相关的判定定理与性质定理.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
如图1,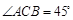 ,
,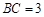 ,过动点A作
,过动点A作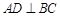 ,垂足
,垂足 在线段
在线段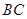 上且异于点
上且异于点 ,连接
,连接 ,沿
,沿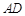 将△
将△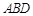 折起,使
折起,使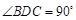 (如图2所示).
(如图2所示). 
(1)当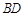 的长为多少时,三棱锥
的长为多少时,三棱锥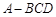 的体积最大;
的体积最大;
(2)当三棱锥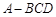 的体积最大时,设点
的体积最大时,设点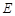 ,
,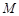 分别为棱
分别为棱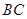 、
、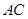 的中点,试在棱
的中点,试在棱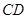 上确定一点
上确定一点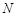 ,使得
,使得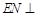
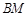 ,并求
,并求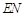 与平面
与平面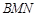 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于点P. 设AB="x," 求△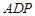 的最大面积及相应的x值.
的最大面积及相应的x值.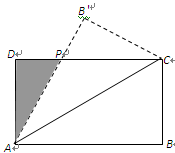
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
如图,在直三棱柱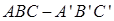 中,
中,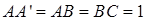 ,
,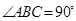 .棱
.棱 上有两个动点E,F,且EF =" a" (a为常数).
上有两个动点E,F,且EF =" a" (a为常数).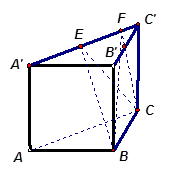
(Ⅰ)在平面ABC内确定一条直线,使该直线与直线CE垂直;
(Ⅱ)判断三棱锥B—CEF的体积是否为定值.若是定值,求出这个三棱锥的体积;若不是定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
下列三个图中,左边是一个正方体截去一个角后所得多面体的直观图。右边两个是正视图和侧视图.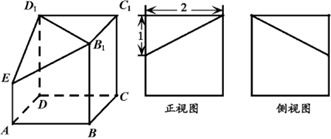
(1)请在正视图的下方,按照画三视图的要求画出该多面体的俯视图(不要求叙述作图过程);
(2)求该多面体的体积(尺寸如图).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com