练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．101（9）化为十进制数为（　　）
    A．9B．11C．82D．101

    分析 利用累加权重法，即可将九进制数转化为十进制，从而得解．

    解答 解：由题意，101（9）=1×92+0×91+1×90=82，
    故选：C．

    点评 本题考查九进制与十进制之间的转化，熟练掌握九进制与十进制之间的转化法则是解题的关键，属于基本知识的考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

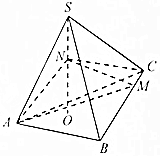    11．如图在三棱锥S-ABC中，CA=CB=3，∠ACB=30°，高SO=8，动点M、N分别在线段BC上SO上，且SN=2CM=2x，则下列四个图象中大致描绘了四面体AMCN的体积V与x变化关系（其中x∈（0，3]）的是（　　）
    A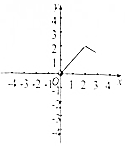．B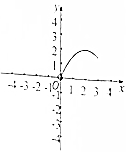．C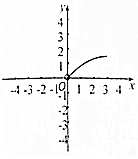．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=lnx-$\frac{ax+1}{x-1}$，a∈R，且f'（2）=$\frac{5}{2}$．
    （1）求函数f（x）的单调区间；
    （2）证明：与曲线y=lnx（x＞1）和y=ex都相切的直线有且只有一条．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．下列命题成立的是（　　）
    A．若￢p、￢q均为真命题，则p∨q为真命题
    B．命题“若x2+2x＜0，则-2＜x＜0”的逆否命题为“若-2＜x＜0，则x2+2x＜0”
    C．方程x2=1的一个必要不充分条件是x=1
    D．抛掷3枚质地均匀的硬币，事件“至少有两枚硬币正面向上”等价于“至多有一枚硬币反面向上”

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知双曲线C1：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为抛物线C2：y2=2px的焦点F，且点F到双曲线的一条渐近线的距离为$\sqrt{3}$，若双曲线C1与抛物线C2在第一象限内的交点为P（x0，2$\sqrt{6}$），则该双曲线的离心率e为（　　）
    A．$\sqrt{2}$B．2C．$\sqrt{3}$D．1+$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．在△ABC中，三个内角A、B、C成等差数列，且cosA=$\frac{2}{3}$，则sinC=（　　）
    A．$\frac{-2\sqrt{3}+\sqrt{5}}{6}$B．$\frac{2\sqrt{3}+\sqrt{5}}{6}$C．$\frac{2\sqrt{3}-\sqrt{5}}{6}$D．$\frac{-2\sqrt{3}-\sqrt{5}}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知数列{an}与{bn}的前n项和分别为An和Bn，且对任意n∈N*，an+1-an=2（bn+1-bn）恒成立．
    （1）若An=n2，b1=2，求Bn；
    （2）若对任意n∈N*，都有an=Bn及$\frac{{b}_{2}}{{a}_{1}{a}_{2}}$+$\frac{{b}_{3}}{{a}_{2}{a}_{3}}$+$\frac{{b}_{4}}{{a}_{3}a4}$+…+$\frac{{b}_{n+1}}{{a}_{n}{a}_{n+1}}$＜$\frac{1}{3}$成立，求正实数b1的取值范围；
    （3）若a1=2，bn=2n，是否存在两个互不相等的整数s，t（1＜s＜t），使$\frac{{A}_{1}}{{B}_{1}}$，$\frac{{A}_{s}}{{B}_{s}}$，$\frac{{A}_{t}}{{B}_{t}}$成等差数列？若存在，求出s，t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．双曲线E1：$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1，F2，椭圆E2：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与双曲线E1有公共的焦点，且E1，E2在第一象限和第四象限的交点分别为M，N，弦MN过F2，则椭圆E2的标准方程为（　　）
    A．$\frac{{x}^{2}}{\frac{81}{4}}$+$\frac{{y}^{2}}{\frac{45}{4}}$=1B．$\frac{{x}^{2}}{13}$+$\frac{{y}^{2}}{4}$=1C．$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{7}$=1D．$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．若函数y=ex+ax有大于零的极值点，则实数a的取值范围是（　　）
    A．a＞-1B．$a＞-\frac{1}{e}$C．a＜-1D．$a＜-\frac{1}{e}$

    查看答案和解析>>

    同步练习册答案