

 =
= ----------------4分
----------------4分 B的概率为:
B的概率为: =
= -------------6分
-------------6分 的值。则
的值。则 就是取出的两个球是不同颜色的概率的近似值。---9分
就是取出的两个球是不同颜色的概率的近似值。---9分

科目:高中数学 来源:不详 题型:解答题
 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: 的分布列和数学期望;
的分布列和数学期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 项技能测试(技能测试项目的顺序固定),假设该员工在每一项技能测试中获得优秀的概率均为0.9,且不同技能测试是否获得优秀相互独立.该员工所在公司规定:三项均获得优
项技能测试(技能测试项目的顺序固定),假设该员工在每一项技能测试中获得优秀的概率均为0.9,且不同技能测试是否获得优秀相互独立.该员工所在公司规定:三项均获得优 秀则奖励
秀则奖励 千元,有
千元,有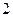 项获得优秀奖励
项获得优秀奖励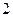 千元,一项获得优秀奖励
千元,一项获得优秀奖励 千元,没有项目获得优秀则没有奖励.记
千元,没有项目获得优秀则没有奖励.记 为该员工通过技能测试获得的奖励金(单位:元).
为该员工通过技能测试获得的奖励金(单位:元). 的分布列;
的分布列; 获得的奖励金
获得的奖励金 的均值.
的均值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com