
【题目】某电信公司从所在地的1000名使用4G手机用户中,随机抽取了20名,对其收集每日使用流量(单位:M)进行统计,得到如下数据:
流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
人数 | 1 | 6 | 6 | 5 | 2 | 0 |
(1)估计这20名4G手机用户每日使用流量(单位:M)的平均值;
(2)估计此地1000名使用4G手机用户中每日使用流量不少于10M用户数;
(3)在15≤x<20和20≤x<25两组用户中,随机抽取两人作进一步问卷调查,求所抽取的两人恰好来自不同组的概率.
【答案】解:(1)![]() =
=![]() (1×2.5+6×7.5+6×12.5+5×17.5+2×22.5)=12.75,
(1×2.5+6×7.5+6×12.5+5×17.5+2×22.5)=12.75,
(2)20名4G手机用户每日使用流每日使用流量不少于10M用户数为20﹣1﹣6=13,
设1000名使用4G手机用户中每日使用流量不少于10M用户数为x,则![]() =
=![]() ,解得x=650,
,解得x=650,
(3)设15≤x<20的5户分别记A,B,C,D,E,20≤x<25的2户分别记为a,b,随机抽取两人,共有21种,分别为AB,AC,AD,AE,Aa,Ab,BC,BD,BE,Ba,Bb,CD,CE,Ca.Cb,DE,Da,Db,Ea,Eb,ab,所抽取的两人恰好来自不同组有10种,分别为Aa,Ab,Ba,Bb,Ca.Cb,Da,Db,Ea,Eb.
故所抽取的两人恰好来自不同组的概率p=![]() .
.
【解析】(1)根据平均数的计算公式计算出平均数,即可估计这20名4G手机用户每日使用流量(单位:M)的平均值;
(2)设1000名使用4G手机用户中每日使用流量不少于10M用户数为x,则![]() =
=![]() , 解得x=650,问题得以解决;
, 解得x=650,问题得以解决;
(3)设15≤x<20的5户分别记A,B,C,D,E,20≤x<25的2户分别记为a,b,随机抽取两人,共有21种,所抽取的两人恰好来自不同组有10种,根据概率公式计算即可.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(Ⅰ)证明:平面ACD⊥平面ABC;
(Ⅱ)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D﹣AE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以坐标原点
为极点,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线
轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若曲线![]() 上的点到直线
上的点到直线![]() 的最大距离为6,求实数
的最大距离为6,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从含有两件正品![]() ,
,![]() 和一件次品
和一件次品![]() 的3件产品中每次任取一件,连续取两次,求取出的两件产品中恰有一件是次品的概率.
的3件产品中每次任取一件,连续取两次,求取出的两件产品中恰有一件是次品的概率.
(1)每次取出不放回;
(2)每次取出后放回.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD=2,P为平面ABCD外一点,且PB⊥BD.
(1)求证:PA⊥BD;
(2)若直线l过点P,且直线l∥直线BC,试在直线l上找一点E,使得直线PC∥平面EBD;
(3)若PC⊥CD,PB=4,求四棱锥P﹣ABCD的体积.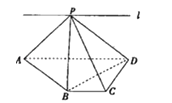
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界那么大,我想去看看,处在具有时尚文化代表的大学生们旅游动机强烈,旅游可支配收入日益增多,可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的![]() 名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该所大学共有学生
,若该所大学共有学生![]() 人,试估计有多少位同学旅游费用支出在
人,试估计有多少位同学旅游费用支出在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中旅游费用支出在![]() 范围内的
范围内的![]() 名学生中有
名学生中有![]() 名女生,
名女生, ![]() 名男生,现想选其中
名男生,现想选其中![]() 名学生回访,记选出的男生人数为
名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE、BE,∠APE的平分线与AE、BE分别交于点C、D,其中∠AEB=30°. 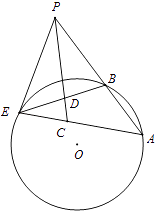
(1)求证: ![]()
(2)求∠PCE的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com