
【题目】已知抛物线![]()
![]() ,过直线
,过直线![]() :
:![]() 上任一点
上任一点![]() 向抛物线
向抛物线![]() 引两条切线
引两条切线![]() (切点为
(切点为![]() ,且点
,且点![]() 在
在![]() 轴上方).
轴上方).
(1)求证:直线![]() 过定点,并求出该定点;
过定点,并求出该定点;
(2)抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知n是一个三位正整数,若n的个位数字大于十位数字,十位数字大于百位数字,则称n为“三位递增数”(如135,256,345等)
现要从甲乙两名同学中,选出一个参加某市组织的数学竞赛,选取的规则如下:从由1,2,3,4,5,6组成的所有“三位递增数”中随机抽取1个数,且只抽取1次,若抽取的“三位递增数”是偶数,则甲参加数学竞赛;否则,乙参加数学竞赛.
(1)由1,2,3,4,5,6可组成多少“三位递增数”?并一一列举出来.
(2)这种选取规则对甲乙两名学生公平吗?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 经过抛物线
经过抛物线![]() 的焦点且与此抛物线交于
的焦点且与此抛物线交于![]() ,
,![]() 两点,
两点,![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() 两点在
两点在![]() 轴的两侧.
轴的两侧.
(1)证明:![]() 为定值;
为定值;
(2)求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(3)若![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某学生在4月份开始进人冲刺复习至高考前的5次大型联考数学成绩(分);

(1)请画出上表数据的散点图;
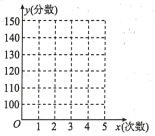
(2)①请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
②若在4月份开始进入冲刺复习前,该生的数学分数最好为116分,并以此作为初始分数,利用上述回归方程预测高考的数学成绩,并以预测高考成绩作为最终成绩,求该生4月份后复习提高率.(复习提高率=![]() ,分数取整数)
,分数取整数)
附:回归直线的斜率和截距的最小二乘估计公式分别为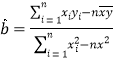 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”。随着经济的发展,我国更加重视对生态环境的保护,2018年起,政府对环保不达标的养鸡场进行限期整改或勒令关闭。一段时间内,鸡蛋的价格起伏较大(不同周价格不同)。假设第一周、第二周鸡蛋的价格分别为![]() 元、
元、![]() 元(单位:kg);甲、乙两人的购买方式不同:甲每周购买3kg鸡蛋,乙每周购买10元钱鸡蛋.
元(单位:kg);甲、乙两人的购买方式不同:甲每周购买3kg鸡蛋,乙每周购买10元钱鸡蛋.
(Ⅰ)若![]() ,求甲、乙两周购买鸡蛋的平均价格;
,求甲、乙两周购买鸡蛋的平均价格;
(Ⅱ)判断甲、乙两人谁的购买方式更实惠(平均价格低视为实惠),并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com