
【题目】任意连结正六边形的6个顶点组成一条闭折线.求证当中必有两条边是平行的.
【答案】见解析
【解析】
用![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 代表六个顶点,
代表六个顶点,
由图可见,两两连线的15条线段可以分为六类平行线:
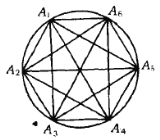
(1)![]() ,其下标满足
,其下标满足![]() .
.
(2)![]() ,其下标满足
,其下标满足![]() .
.
(3)![]() ,其下标满足
,其下标满足![]() .
.
(4)![]() ,其下标满足
,其下标满足![]() .
.
(5)![]() ,其下标满足
,其下标满足![]() .
.
(6)![]() ,其下标满足
,其下标满足![]() .
.
由此可以得出两个结论:
结论1 两条线段![]() 的充要条件是
的充要条件是![]() .
.
如图,有![]()
![]() .
.
结论2 六类平行线恰好对应着模6的六个剩余1,2,3,4,5,0.
由于封闭折线上的每一点都是两条线段的端点,因而其六条线段上各端点下标之和为
![]() . ①
. ①
若封闭折线上的六条边分别取自上述六类(每类一条),
则其端点下标之和关于模6取遍1,2,3,4,5,0,有![]() .
.
这与①矛盾.所以,封闭折线上的六条边最多取自五类,至少有两条边属于同一类,这同一类的边就互相平行.


科目:高中数学 来源: 题型:
【题目】如图,在直角三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() .
.
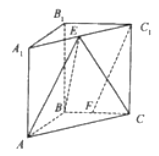
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若直线![]() 和平面
和平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
(1)该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
(2)若某顾客购物金额为180元,选择哪种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1998年,某地在抗洪抢险中接到预报,24小时后有一个超历史最高水位的洪峰到达,为保万无一失,指挥部决定在24小时内筑起一道堤坝作为第二防线.经计算,其工程量除动用现有军民连续奋战外,还需要20台大型翻斗车同时作业24小时.但是,除了第一辆车可以立即调入工作外,其余车辆需从各单位紧急抽调,每隔20分钟有一辆车到达投入作业,已知指挥部最多能组织到25辆车.问24小时内能否完成第二防线工程?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.
元.
该公司将近![]() 天,每天揽件数量统计如下:
天,每天揽件数量统计如下:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
(1)某人打算将![]() ,
, ![]() ,
, ![]() 三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过
三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过![]() 元的概率;
元的概率;
(2)该公司从收取的每件快递的费用中抽取![]() 元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过
元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过![]() 件,工资
件,工资![]() 元,目前前台有工作人员
元,目前前台有工作人员![]() 人,那么,公司将前台工作人员裁员
人,那么,公司将前台工作人员裁员![]() 人对提高公司利润是否更有利?
人对提高公司利润是否更有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着“一带一路”倡议的推进,中国与沿线国家旅游合作越来越密切,中国到“一带一路”沿线国家的游客人也越来越多,如图是2013-2018年中国到“一带一路”沿线国家的游客人次情况,则下列说法正确的是( )
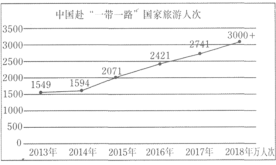
①2013-2018年中国到“一带一路”沿线国家的游客人次逐年增加
②2013-2018年这6年中,2016年中国到“一带一路”沿线国家的游客人次增幅最小
③2016-2018年这3年中,中国到“一带一路”沿线国家的游客人次每年的增幅基本持平
A.①③B.②③C.①②D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为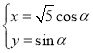 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时
的最小值及此时![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对本工厂工人的理论成绩与实践能力进行分析,决定从本工厂工人中随机抽取一个样本容量为7的样本进行分析.如果随机抽取的7名工人的理论成绩与实践能力值![]() 单位:分
单位:分![]() 对应如下表:
对应如下表:
工人序号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
理论成绩 | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
实践能力值 | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
(1)求这7名工人的理论成绩![]() 与实践能力值
与实践能力值![]() 的中位数、极差;
的中位数、极差;
(2)若规定85分以上![]() 包括85分
包括85分![]() 为优秀,从这7名工人中抽取3名工人,记3名工人中理论成绩和实践能力值均为优秀的人数为X,求X的分布列和期望;
为优秀,从这7名工人中抽取3名工人,记3名工人中理论成绩和实践能力值均为优秀的人数为X,求X的分布列和期望;
(3)根据下表数据,求实践能力值y关于理论成绩x的线性回归方程.![]() 系数精确到
系数精确到![]()
附:线性回归方程![]() 中,
中,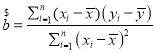 ,
,![]() .
.
|
|
|
|
76 | 83 | 812 | 526 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com