
【题目】已知函数![]() .
.
(1)讨论![]() 时,函数
时,函数![]() 的单调性;
的单调性;
(2)若![]() ,函数
,函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递减. 当
上单调递减. 当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减. (2)
上单调递减. (2)![]()
【解析】
(1)当![]() 时,求出函数
时,求出函数![]() 的导函数
的导函数![]() ,讨论
,讨论![]() 和
和![]() ,对
,对![]() 进行讨论即可.
进行讨论即可.
(2)分离参数得方程![]() 有两个根,设函数
有两个根,设函数![]() ,讨论
,讨论![]() 的单调性,从而可得到答案.
的单调性,从而可得到答案.
(1) 当![]() 时,
时,![]() ,则
,则![]()
当![]() 时,
时,![]() 在
在![]() 上恒成立,则此时
上恒成立,则此时![]() 单调递减.
单调递减.
当![]() 时,由
时,由![]() ,即
,即![]() ,得
,得![]()
由![]() ,即
,即![]() ,得
,得![]() .
.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减..
上单调递减..
(2) 函数![]() 有两个零点,即方程
有两个零点,即方程![]() 有两个根.
有两个根.
设![]()
则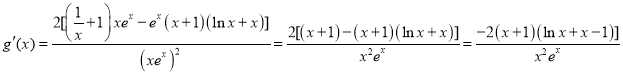
设![]() ,则
,则![]()
所以![]() 在
在![]() 上单调递增且
上单调递增且![]() .
.
所以当![]() 时,
时,![]() ;当
;当![]() 时.
时. ![]() .
.
所以当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
因此![]() .
.
又当![]() 时,
时,![]() 且
且![]() 时,
时,![]() .
.
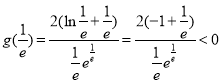
方程![]() 有两个根.
有两个根.
则![]()
所以函数![]() 有两个零点实数
有两个零点实数![]() 的取值范围是
的取值范围是![]() .
.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据茎叶如图所示.
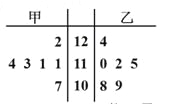
(Ⅰ)根据样本数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对稳定;
(Ⅱ)若从乙车间![]() 件样品中随机抽取两件,求所抽取两件样品重量之差不超过
件样品中随机抽取两件,求所抽取两件样品重量之差不超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《孙子算经》中记有如下问题:“今有五等诸侯,其分橘子六十颗,人別加三颗”,问:“五人各得几何?”其意思为:“现在有5个人分60个橘子,他们分得的橘子个数成公差为3的等差数列,问5人各得多少橘子.”根据这个问题,下列说法错误的是( )
A.得到橘子最多的诸侯比最少的多12个
B.得到橘子的个数排名为正数第3和倒数第3的是同一个人
C.得到橘子第三多的人所得的橘子个数是12
D.所得橘子个数为倒数前3的诸侯所得的橘子总数为24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是两个小区所在地,
是两个小区所在地,![]() 、
、![]() 到一条公路
到一条公路![]() 的垂直距离分别为
的垂直距离分别为![]()
![]() ,
,![]()
![]() ,
,![]() 两端之间的距离为
两端之间的距离为![]()
![]() .
.
(1)某移动公司将在![]() 之间找一点
之间找一点![]() ,在
,在![]() 处建造一个信号塔,使得
处建造一个信号塔,使得![]() 对
对![]() 、
、![]() 的张角与
的张角与![]() 对
对![]() 、
、![]() 的张角相等,试确定点
的张角相等,试确定点![]() 的位置.
的位置.
(2)环保部门将在![]() 之间找一点
之间找一点![]() ,在
,在![]() 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得![]() 对
对![]() 、
、![]() 所张角最大,试确定点
所张角最大,试确定点![]() 的位置.
的位置.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 图象上的所有点的横坐标伸长到原来的2倍,再把所得各点向右平移
图象上的所有点的横坐标伸长到原来的2倍,再把所得各点向右平移![]() 个单位长度,最后把所得各点纵坐标扩大到原来的2倍,就得到函数f(x)的图象,则下列说法中正确的个数是( )
个单位长度,最后把所得各点纵坐标扩大到原来的2倍,就得到函数f(x)的图象,则下列说法中正确的个数是( )
①函数f(x)的最小正周期为2π;
②函数f(x)的最大值为2;
③函数f(x)图象的对称轴方程为![]() ;
;
④设x1,x2为方程![]() 的两个不相等的根,则
的两个不相等的根,则![]() 的最小值为
的最小值为![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.
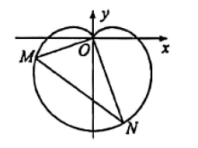
(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com