
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长为
为边长为![]() 的正方形,
的正方形,![]() ,
,![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中.
中.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在棱
在棱![]() 上,满足
上,满足![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 得取值范围.
得取值范围.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设AC的中点为O,连接BO,PO,先证明PO⊥AC,PO⊥OB,可得PO⊥平面ABC,从而可得结论;(2)以OC,OB,OP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,设![]() ,求出
,求出![]() 与
与![]() 的坐标,令
的坐标,令![]() ,得
,得![]() ,化为
,化为![]() ,利用单调性可得结果.
,利用单调性可得结果.
(1)设AC的中点为O,连接BO,PO.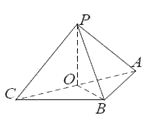
由题意,得PA=PB=PC=![]() ,
,
PO=2,AO=BO=CO=1,
∵在△PAC中,PA=PC,O为AC的中点,∴PO⊥AC,
∵在△POB中,PO=1,OB=1,PB=![]() ,
,
∴PO⊥OB.
∵AC∩OB=O,AC,OB平面ABC,∴PO⊥平面ABC,
∵PO平面PAC,∴平面PAC⊥平面ABC.
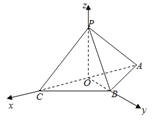
(2)由PO⊥平面ABC,![]() ,如图建立空间坐标系,
,如图建立空间坐标系,
则![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]()
令![]() ,得
,得![]() ,
,
即![]() ,
,![]() 是关于
是关于![]() 的单调递增函数,
的单调递增函数,
当![]() 时,
时,![]() ,
,
故![]() 的取值范围为
的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】△ABC的三内角A,B,C所对的边分别为a,b,c,若cosA=![]() cosB,b=
cosB,b=![]() ,c=4,M,N是边AC上的两个动点,且AM=2CN,则
,c=4,M,N是边AC上的两个动点,且AM=2CN,则![]() 的最大值为______.
的最大值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出的是2017年11月-2018年11月某工厂工业原油产量的月度走势图,则以下说法正确的是( )
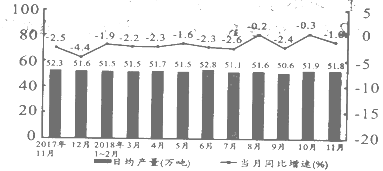
A. 2018年11月份原油产量约为51.8万吨
B. 2018年11月份原油产量相对2017年11月增加1.0%
C. 2018年11月份原油产量比上月减少54.9万吨
D. 2018年1-11月份原油的总产量不足15000万吨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是()
A. 若函数![]() 为奇函数,则
为奇函数,则![]() ;
;
B. 若数列![]() 为常数列,则
为常数列,则![]() 既是等差数列也是等比数列;
既是等差数列也是等比数列;
C. 在![]() 中,
中,![]() 是
是![]() 的充要条件;
的充要条件;
D. 若两个变量![]() 的相关系数为
的相关系数为![]() ,则
,则![]() 越大,
越大,![]() 与
与![]() 之间的相关性越强.
之间的相关性越强.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年东京夏季奥运会将设置![]() 米男女混合泳接力这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳
米男女混合泳接力这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳![]() 蛙泳
蛙泳![]() 蝶泳
蝶泳![]() 自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场,若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者自由泳,剩下的2名运动员四种泳姿都可以承担,则中国队的排兵布阵的方式共有( )
自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场,若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者自由泳,剩下的2名运动员四种泳姿都可以承担,则中国队的排兵布阵的方式共有( )
A. 144种B. 24种C. 12种D. 6种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 中,
中,![]() 菱形
菱形![]() 所在的平面,
所在的平面,![]() 是
是![]() 中点,
中点,![]() 是
是![]() 上的点.
上的点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,当
的中点,当![]() 时,是否存在点
时,是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 的所成角的正弦值为
的所成角的正弦值为![]() ?若存在,请求出
?若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]()
![]() ,过焦点F的直线l与抛物线交于S,T,且
,过焦点F的直线l与抛物线交于S,T,且![]() .
.

(1)求抛物线C的方程;
(2)设点P是x轴下方(不含x轴)一点,抛物线C上存在不同的两点A,B满足![]()
![]() ,其中
,其中![]() 为常数,且两点D,E均在C上,弦AB的中点为M.
为常数,且两点D,E均在C上,弦AB的中点为M.
①若点P坐标为![]()
![]() ,抛物线过点A,B的切线的交点为N,证明:点N在直线MP上;
,抛物线过点A,B的切线的交点为N,证明:点N在直线MP上;
②若直线PM交抛物线于点Q,求证;![]() 为定值(定值用
为定值(定值用![]() 表示).
表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com