Question

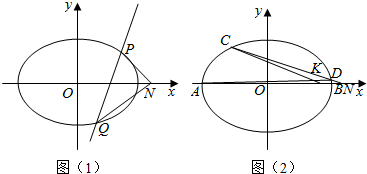
19．椭圆C的方程为：$\frac{{x}^{2}}{2}$+y²=1．
（I）直线l：x=my+1与椭圆C交于不同的两点P、Q，在x轴上存在定点N，使得x轴平分∠PNQ，求出点N的坐标．
（Ⅱ）设椭圆的左右顶点为A，B．过点N作直线l′交椭圆C于不同的两点C，D，直线AD，BC交于点K．证明点K在一条定直线上．

Answer 1

分析 （I）设N（t，0），P（x₁，y₁），Q（x₂，y₂）．由于x轴平分∠PNQ，可得k_PN+k_QN=0．化为：2my₁y₂+（1-t）（y₁+y₂）=0．直线方程与椭圆方程联立化为：（m²+2）y²+2my-1=0，把根与系数的关系代入化简即可得出．
（II）A（-$\sqrt{2}$，0），B$（\sqrt{2}，0）$，N（2，0），C（x₃，y₃），D（x₄，y₄），设直线l′：ny+2=x．与椭圆方程联立化为（n²+2）y²+4ny+2=0．直线AD的方程为：y-0=$\frac{{y}_{4}}{{x}_{4}+\sqrt{2}}$$（x+\sqrt{2}）$，直线BC的方程为：y-0=$\frac{{y}_{3}}{{x}_{3}-\sqrt{2}}$$（x-\sqrt{2}）$．联立解得：x=$\frac{\sqrt{2}[2n{y}_{3}{y}_{4}+2（{y}_{3}+{y}_{4}）+\sqrt{2}（{y}_{3}-{y}_{4}）]}{\sqrt{2}（{y}_{3}+{y}_{4}）+2（{y}_{3}-{y}_{4}）}$，把根与系数的关系代入即可得出．

解答 （I）解：设N（t，0），P（x₁，y₁），Q（x₂，y₂），
∵x轴平分∠PNQ，∴k_PN+k_QN=0．
∴$\frac{{y}_{1}}{{x}_{1}-t}$+$\frac{{y}_{2}}{{x}_{2}-t}$=0，又x₁=my₁+1，x₂=my₂+1．
化为：2my₁y₂+（1-t）（y₁+y₂）=0．（*）
联立$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$，化为：（m²+2）y²+2my-1=0，
△=4m²+4（m²+2）＞0．
∴y₁+y₂=$\frac{-2m}{{m}^{2}+2}$，y₁y₂=$\frac{-1}{{m}^{2}+2}$．
代入（*）可得：m（t-2）=0，
由于m可以变化，∴t=2．
∴N（2，0）．
（II）证明：A（-$\sqrt{2}$，0），B$（\sqrt{2}，0）$，N（2，0），C（x₃，y₃），D（x₄，y₄），
设直线l′：ny+2=x．
联立$\left\{\begin{array}{l}{ny+2=x}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$，化为（n²+2）y²+4ny+2=0．
△=16n²-8（n²+2）＞0，化为：n²＞2．
∴y₃+y₄=$\frac{-4n}{{n}^{2}+2}$，y₃y₄=$\frac{2}{{n}^{2}+2}$．
直线AD的方程为：y-0=$\frac{{y}_{4}}{{x}_{4}+\sqrt{2}}$$（x+\sqrt{2}）$，
直线BC的方程为：y-0=$\frac{{y}_{3}}{{x}_{3}-\sqrt{2}}$$（x-\sqrt{2}）$．
联立解得：x=$\frac{\sqrt{2}[2n{y}_{3}{y}_{4}+2（{y}_{3}+{y}_{4}）+\sqrt{2}（{y}_{3}-{y}_{4}）]}{\sqrt{2}（{y}_{3}+{y}_{4}）+2（{y}_{3}-{y}_{4}）}$，
∵2ny₃y₄+2（y₃+y₄）=$\frac{4n}{{n}^{2}+2}$-$\frac{8n}{{n}^{2}+2}$=$\frac{-4n}{{n}^{2}+2}$=y₃+y₄，
∴x=$\frac{\sqrt{2}[（{y}_{3}+{y}_{4}）+\sqrt{2}（{y}_{3}-{y}_{4}）]}{\sqrt{2}[（{y}_{3}+{y}_{4}）+\sqrt{2}（{y}_{3}-{y}_{4}）]}$=1，
∴点K在一条定直线x=1上．

点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、斜率计算公式，考查了推理能力与计算能力，属于难题．