
【题目】如图,菱形![]() 与正三角形
与正三角形![]() 的边长均为
的边长均为![]() ,它们所在平面互相垂直,
,它们所在平面互相垂直, ![]() 平面
平面![]() ,且
,且![]() .
.
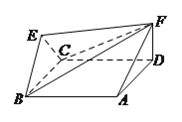
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() ,求几何体
,求几何体![]() 的体积.
的体积.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列命题:①
,给出下列命题:①![]() 必是偶函数;②当
必是偶函数;②当![]() 时,
时,![]() 的图像关于直线
的图像关于直线![]() 对称;③若
对称;③若![]() ,则
,则![]() 在区间
在区间![]() 上是增函数;④若
上是增函数;④若![]() ,在区间
,在区间![]() 上
上![]() 有最大值
有最大值![]() . 其中正确的命题序号是:( )
. 其中正确的命题序号是:( )
A. ③ B. ②③ C. ③④ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c,满足f(0)=2,f(x+1)-f(x)=2x-1.
(1)求函数f(x)的解析式;
(2)求f(x)在区间 [-1,2]上的最大值;
(3)若函数f(x)在区间![]() 上单调,求实数
上单调,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax(a>0,a≠1)在区间[﹣1,2]上的最大值为8,最小值为m.若函数g(x)=(3﹣10m) ![]() 是单调增函数,则a= .
是单调增函数,则a= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点R(x0 , y0)在D:y2=2px上,以R为切点的D的切线的斜率为 ![]() ,过Γ外一点A(不在x轴上)作Γ的切线AB、AC,点B、C为切点,作平行于BC的切线MN(切点为D),点M、N分别是与AB、AC的交点(如图).
,过Γ外一点A(不在x轴上)作Γ的切线AB、AC,点B、C为切点,作平行于BC的切线MN(切点为D),点M、N分别是与AB、AC的交点(如图).
(1)用B、C的纵坐标s、t表示直线BC的斜率;
(2)设三角形△ABC面积为S,若将由过Γ外一点的两条切线及第三条切线(平行于两切线切点的连线)围成的三角形叫做“切线三角形”,如△AMN,再由M、N作“切线三角形”,并依这样的方法不断作切线三角形…,试利用“切线三角形”的面积和计算由抛物线及BC所围成的阴影部分的面积T.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(﹣1)=0,当x>0时,xf′(x)﹣f(x)<0,则使得f(x)>0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(﹣1,0)
D.(0,1)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C1的参数方程为 ![]() ,(α为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+
,(α为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+ ![]() )=4
)=4 ![]() .
.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)设P为曲线C1上的动点,求点P到C2上点的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() (
(![]() ,
,![]() )具有性质
)具有性质![]() :对任意
:对任意![]() 、
、![]() (
(![]() ),
),![]() 与
与![]() 两数中至少有一个属于集合
两数中至少有一个属于集合![]() ,现给出以下四个命题:①数集
,现给出以下四个命题:①数集![]() 具有性质
具有性质![]() ;②数集
;②数集![]() 具有性质
具有性质![]() ;③若数集
;③若数集![]() 具有性质
具有性质![]() ,则
,则![]() ;④若数集
;④若数集![]() (
(![]() )具有性质
)具有性质![]() ,则
,则![]() ;其中真命题有________(填写序号)
;其中真命题有________(填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com