
【题目】据市场调查发现,某种产品在投放市场的30天中,其销售价格![]() (元)和时间
(元)和时间![]() (天)的关系如图所示.
(天)的关系如图所示.

(1)求销售价格![]() (元)和时间
(元)和时间![]() (天)的函数关系式;
(天)的函数关系式;
(2)若日销售量![]() (件)与时间
(件)与时间![]() (天)的函数关系式是
(天)的函数关系式是![]()
![]() ,问该产品投放市场第几天时,日销售额
,问该产品投放市场第几天时,日销售额![]() (元)最高,且最高为多少元?
(元)最高,且最高为多少元?
【答案】(Ⅰ)![]() ;(Ⅱ)在第10天时,日销售额最大,最大值为900元.
;(Ⅱ)在第10天时,日销售额最大,最大值为900元.
【解析】
试题(Ⅰ)通过讨论t的范围,求出函数的表达式即可;(Ⅱ)先求出函数的表达式,通过讨论t的范围,求出函数的最大值即可.
解:(Ⅰ)①当0≤t<20,t∈N时,
设P=at+b,将(0,20),(20,40)代入,得![]() 解得
解得![]()
所以P=t+20(0≤t<20,t∈N).
②当20≤t≤30,t∈N时,
设P=at+b,将(20,40),(30,30)代入,解得![]()
所以 P=﹣t+60(20≤t≤30,t∈N),)
综上所述![]()
(Ⅱ)依题意,有y=PQ,
得![]()
化简得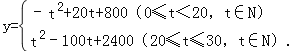
整理得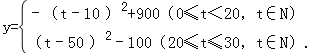
①当0≤t<20,t∈N时,由y=﹣(t﹣10)2+900可得,当t=10时,y有最大值900元.
②当20≤t≤30,t∈N时,由y=(t﹣50)2﹣100可得,当t=20时,y有最大值800元.
因为 900>800,所以在第10天时,日销售额最大,最大值为900元.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,其中c为常数,且函数f(x)的图象过原点.
,其中c为常数,且函数f(x)的图象过原点.
(1)求c的值,并求证:f(![]() )+f(x)=1;
)+f(x)=1;
(2)判断函数f(x)在(-1,+∞)上的单调性,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价为5元,销售单价与日均销售量的关系如图所示.
销售单价/元 | … | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | … |
日均销售量/桶 | … | 480 | 460 | 440 | 420 | 400 | 380 | … |
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( ) 
A.9
B.18
C.20
D.35
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:![]() ,直线
,直线![]() 过定点
过定点![]() .
.
(1)若![]() 与圆相切,求
与圆相切,求![]() 的方程;
的方程;
(2)若![]() 与圆相交于
与圆相交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,又
,又![]() 与
与![]() 的交点为
的交点为![]() ,判断
,判断![]() 是否为定值.若是,求出定值;若不是,请说明理由.
是否为定值.若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=2(cos θ+sin θ).
(1)求C的直角坐标方程;
(2)直线l: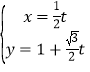 (t为参数)与曲线C交于A,B两点,与y轴交于点E,求|EA|+|EB|.
(t为参数)与曲线C交于A,B两点,与y轴交于点E,求|EA|+|EB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在S市的A区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
x(个) | 2 | 3 | 4 | 5 | 6 |
y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
(1)在年收入之和为2.5(百万元)和3(百万元)两区中抽取两分店调查,求这两分店来自同一区的概率
(2)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(3)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为z=y-0.05x2-1.4,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店,才能使A区平均每个分店的年利润最大?
参考公式:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com