
分析 (1)由$\frac{x-2a}{x+2a}>0$,解得:函数f(x)的定义域,再由函数奇偶性的定义,可判断出f(x)为奇函数.
(2)若对任意x∈D,不等式|h(x)|≤2恒成立,即为|${log_a}(-{x^2}+6ax-8{a^2})$|≤2恒成立,分类求出各种情况下满足条件的a值,综合可得实数a的取值范围.
解答 解:(1)由$\frac{x-2a}{x+2a}>0$,整理得(x+2a)(x-2a)>0,解得x<-2a,或x>2a,
∴f(x)的定义域为(-∞,-2a)∪(2a,+∞).…(2分)
又∵$f(x)+f(-x)={log_a}\frac{x-2a}{x+2a}+{log_a}\frac{-x-2a}{-x+2a}$=${log_a}(\frac{x-2a}{x+2a}•\frac{x+2a}{x-2a})={log_a}1=0$,
∴f(-x)=f(x),
∴f(x)为奇函数.…(4分)
(2)由已知3a∉[2a+1,2a+$\frac{3}{2}$],
∴2a+1>3a,或2a+$\frac{3}{2}$<3a,即0<a<1,或a>$\frac{3}{2}$. …(5分)
又∵要使g(x)有意义,就须使x+2a>0,且4a-x>0,即-2a<x<4a,
结合(1)中f(x)的定义域知函数h(x)的自变量x须满足2a<x<4a.
由题知h(x)在区间[2a+1,2a+$\frac{3}{2}$]上有意义,
∴$\left\{\begin{array}{l}2a+1>2a\\ 2a+\frac{3}{2}<4a\end{array}\right.$解得a>$\frac{3}{4}$,
∴$\frac{3}{4}$<a<1,或a>$\frac{3}{2}$.…(6分)
∵h(x)=f(x)+g(x)=${log_a}\frac{x-2a}{x+2a}$+loga(x+2a)+loga(4a-x)=${log_a}(-{x^2}+6ax-8{a^2})$,
∴|h(x)|≤2恒成立,即为|${log_a}(-{x^2}+6ax-8{a^2})$|≤2恒成立.
因为 3a∉[2a+1,2a+$\frac{3}{2}$],所以h(x)≠2,
即题意转化为对任意x∈[2a+1,2a+$\frac{3}{2}$],不等式-2≤${log_a}(-{x^2}+6ax-8{a^2})<2$应恒成立.
…(7分)
①当$\frac{3}{4}<a<1$时,上式等价于a2<-x2+6ax-8a2≤a-2应恒成立.
由于左端a2<-x2+6ax-8a2,即(x-3a)2<0,显然不成立.…(8分)
②当$a>\frac{3}{2}$时,问题转化为a-2≤-x2+6ax-8a2<a2应恒成立.
对于右端-x2+6ax-8a2<a2,等价于(x-3a)2>0,显然成立.
研究左端${x^2}-6ax+8{a^2}+\frac{1}{a^2}$≤0成立的条件.
令$h(x)={x^2}-6ax+8{a^2}+\frac{1}{a^2}={(x-3a)^2}-{a^2}+\frac{1}{a^2}$,对称轴x=3a,开口向上.
由$a>\frac{3}{2}$知$2a+\frac{3}{2}<3a$,故h(x)在区间[2a+1,2a+$\frac{3}{2}$]上是减函数,
∴h(x)max=h(2a+1),
∴要使左端成立,只需h(2a+1)<0成立,
即需${(2a+1)^2}-6a(2a+1)+8{a^2}+\frac{1}{a^2}<0$,
也就是需2a3-a2-1>0,
也就是(a-1)(2a2+a+1)>0,
只须a>1,而已知$a>\frac{3}{2}$,故当$a>\frac{3}{2}$时,不等式a-2≤-x2+6ax-8a2<a2恒成立.
综上所述,满足条件的a的取值范围为($\frac{3}{2}$,+∞).…(10分)
点评 本题考查的知识点是函数的定义域,函数的奇偶性,函数恒成立问题,函数的最值,难度中档.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是奇函数,则在(0,+∞)上是增函数 | |
| B. | f(x)是偶函数,则在(0,+∞)上是减函数 | |
| C. | f(x)既不是奇函数也不是偶函数,且在(0,+∞)上是增函数 | |
| D. | f(x)既不是奇函数也不是偶函数,且在(0,+∞)上是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
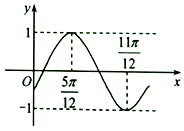 函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(0)=$-\frac{{\sqrt{3}}}{2}$.
函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(0)=$-\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com