
【题目】四棱锥S﹣ABCD的底面ABCD是正方形,各侧棱长与底面的边长均相等,M为SA的中点,则直线BM与SC所成的角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:过点P作PO⊥平面ABCD,交ABCD于点O,
以O为原点,过O作DA的平行线为x轴,过O作AB的平行线为y轴,OS为z轴,建立空间直角坐标系,
如图所示:
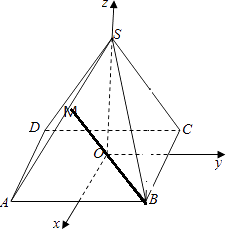
设正四棱锥S﹣ABCD侧棱长与底面边长都为2,
则A(1,﹣1,0),OB= ![]() ,OS=
,OS= ![]() =
= ![]() ,B(1,1,0),
,B(1,1,0),
S(0,0, ![]() ),C(﹣1,1,0),M(
),C(﹣1,1,0),M( ![]() ,﹣
,﹣ ![]() ,
, ![]() ),
),
![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,
, ![]() ),
), ![]() =(﹣1,1,﹣
=(﹣1,1,﹣ ![]() ),
),
设BE与SA所成角为θ,
则cosθ= 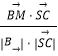 =
= ![]() .
.
∴BM与SC所成角的余弦值为 ![]() .
.
所以答案是:C.
【考点精析】认真审题,首先需要了解异面直线及其所成的角(异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系).


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ax,g(x)=ex﹣3ax,其中a为实数,若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,则a的取值范围是( )
A.( ![]() ,+∞)
,+∞)
B.[ ![]() ,+∞)
,+∞)
C.(1,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=﹣x3+ax2+bx+c的导数f'(x)满足f'(﹣1)=0,f'(2)=9.
(1)求f(x)的单调区间;
(2)f(x)在区间[﹣2,2]上的最大值为20,求c的值.
(3)若函数f(x)的图象与x轴有三个交点,求c的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 ![]() ,方程x2+y2﹣2mx﹣2y+m+3=0表示圆.
,方程x2+y2﹣2mx﹣2y+m+3=0表示圆.
(Ⅰ)求实数m的取值范围;
(Ⅱ)当m=﹣2时,试判断直线l与该圆的位置关系,若相交,求出相应弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个科研小组有4位男组员和2位女组员,其中一位男组员和一位女组员不会英语,其他组员都会英语,现在要用抽签的方法从中选出两名组员组成一个科研攻关小组.
(Ⅰ)求组成攻关小组的成员是同性的概率;
(Ⅱ)求组成攻关小组的成员中有会英语的概率;
(Ⅲ)求组成攻关小组的成员中有会英语并且是异性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位打字员在两台电脑上各自输入A,B两种类型的文件的部分文字才能使这两类文件成为成品.已知A文件需要甲输入0.5小时,乙输入0.2小时;B文件需要甲输入0.3小时,乙输入0.6小时.在一个工作日中,甲至多只能输入6小时,乙至多只能输入8小时,A文件每份的利润为60元,B文件每份的利润为80元,则甲、乙两位打字员在一个工作日内获得的最大利润是元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx﹣cosx)2+ ![]() sin(2x+
sin(2x+ ![]() )(x∈R).
)(x∈R).
(1)求函数f(x)的递减区间;
(2)若f(α)= ![]() ,α∈(
,α∈( ![]() ,
, ![]() ),求cos(2α+
),求cos(2α+ ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义 ![]() 为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为
为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为 ![]() ,又bn=
,又bn= ![]() ,则
,则 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com