练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．BD是等腰直角三角形△ABC腰AC上的中线，AM⊥BD于点M，延长AM交BC于点N，AF⊥BC于点F，AF与BD交于点E．
    （1）求证；△ABE≌△ACN；
    （2）求证：∠ADB=∠CDN．

    分析 （1）通过证明∠BAE=∠C，AB=AC，∠ABD=∠NAC，即可判定△ABE≌△ACN．
    （2）由AE=NC，AD=CD，∠EAD=∠C，可证明△ADE≌△CDN，利用全等三角形的性质即可证明∠ADB=∠CDN．

    解答 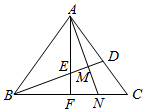（本题满分为10分）
    证明：（1）∠BAE=∠C=45°，
    AB=AC，
    ∠ABD=∠NAC（∠ADB的余角），
    ∴△ABE≌△ACN．…（5分）
    （2）由（1）可得AE=NC，
    AD=CD，∠EAD=∠C=45°，
    ∴△ADE≌△CDN，
    ∴∠ADB=∠CDN．…（10分）

    点评 本题主要考查了全等三角形的判定和性质的应用，考查了转化思想和数形结合思想的应用，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．曲线y=e-x在点（x0，$\frac{1}{e}$）处的切线与坐标轴围成的三角形的面积为$\frac{2}{e}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．某中学为研究学生的身体素质与课外体育锻炼时间的关系，对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查，如表：（平均每天锻炼的时间单位：分钟）
    平均每天锻炼
    的时间（分钟）    		[0，10）[10，20）[20，30）[30，40）[40，50）[50，60）
    总人数203644504010
    将学生日均课外课外体育运动时间在[40，60）上的学生评价为“课外体育达标”．
    （Ⅰ）请根据上述表格中的统计数据填写下面2×2列联表，并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关？
    课外体育不达标课外体育达标合计
    男
    女20110
    合计
    （Ⅱ）将上述调查所得到的频率视为概率．现在从该校高三学生中，抽取3名学生，记被抽取的3名学生中的“课外体育达标”学生人数为X，若每次抽取的结果是相互独立的，求X的数学期望和方差．
    参考公式：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d．
    参考数据：
    P（K2≥k0）0.100.050.0250.0100.0050.001
    k02.7063.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设函数f（x）=$\frac{1}{2}$x2-9lnx在区间[a-$\frac{1}{2}$，a+$\frac{1}{2}$]上单调递减，则实数a的取值范围是（$\frac{1}{2}$，$\frac{5}{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

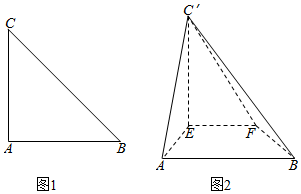    7．如图1，△ABC是等腰直角三角形∠CAB=90°，AC=2a，E，F分别为AC，BC的中点，沿EF将△CEF折起，得到如图2所示的四棱锥C′-ABFE
    （Ⅰ）求证：AB⊥平面AEC′；
    （Ⅱ）当四棱锥C′-ABFE体积取最大值时，
    （i）若G为BC′中点，求异面直线GF与AC′所成角；
    （ii）在C′-ABFE中AE交BF于C，求二面角A-CC′-B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=$\sqrt{3}$sin（ωx+φ）-cos（ωx+φ）（0＜φ＜π，ω＞0）为偶函数，且函数y=f（x）图象的两相邻对称轴间的距离为$\frac{π}{2}$．
    （1）求f（$\frac{π}{4}$-α）=$\frac{3\sqrt{7}}{4}$，α∈（$\frac{π}{4}$，$\frac{π}{2}$），求sinα的值；
    （2）将函数y=f（x）的图象向右平移$\frac{π}{6}$个单位长度后，再将得到的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，得到函数y=g（x）的图象，求g（x）在[-π，π]上的单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知各项均为正数的两个数列{an}和{bn}满足：an+1=$\frac{{a}_{n}+{b}_{n}}{\sqrt{{a}_{n}^{2}+{b}_{n}^{2}}}$，bn+1=1+$\frac{{b}_{n}}{{a}_{n}}$，n∈N*，
    （1）求证：数列{（$\frac{{b}_{n}}{{a}_{n}}$）2}是等差数列；
    （2）若a1=b1=1令（$\frac{{b}_{n}}{{a}_{n}}$）2=$\frac{1}{{c}_{n}}$，若Sn=C1C2+C2C3+…+CnCn+1，求Sn；
    （3）在（2）的条件下，设dn=$\frac{3-{S}_{n-1}}{1-\sqrt{11}（1-{S}_{n-1}）}$，若dn≤2m-1，对于任意的n∈N+恒成立，求正整数m的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知m，n是两条不同的直线，α，β是两个不同的平面，若m⊥α，n⊥β，且β⊥α，则下列结论一定正确的是（　　）
    A．m⊥nB．m∥nC．m与n相交D．m与n异面

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．分子为1且分母为正整数的分数称为单位分数．1可以分拆为若干个不同的单位分数之和：
    1=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{6}$，
    1=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{12}$，
    1=$\frac{1}{2}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$，
    …，
    依此类推可得：1=$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{m}$+$\frac{1}{n}$+$\frac{1}{30}$+$\frac{1}{42}$+$\frac{1}{56}$+$\frac{1}{72}$+$\frac{1}{90}$+$\frac{1}{110}$+$\frac{1}{132}$+$\frac{1}{156}$，其中，m、n∈N*，则mn=（　　）
    A．228B．240C．260D．273

    查看答案和解析>>

    同步练习册答案