
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源:不详 题型:解答题
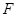 、
、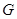 的函数
的函数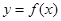 、
、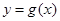 ,
,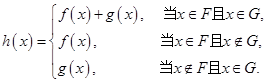
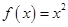 ,
,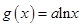
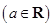 .
.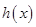 的解析式;
的解析式;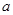 ,函数
,函数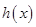 是否存在最小值,如果存在,求出其最小值;如果不存在,请说明理由.
是否存在最小值,如果存在,求出其最小值;如果不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
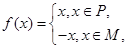 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断: ,则f(P)∩f(M)=
,则f(P)∩f(M)= ;
; ,则f(P)∩f(M) ≠
,则f(P)∩f(M) ≠ ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
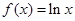 ,
,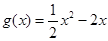 .
.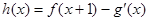 (其中
(其中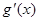 是
是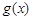 的导函数),求
的导函数),求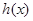 的最大值;
的最大值;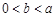 时,有
时,有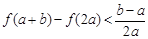 ;
;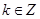 ,当
,当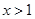 时,不等式
时,不等式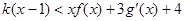 恒成立,求
恒成立,求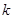 的最大值.
的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com