
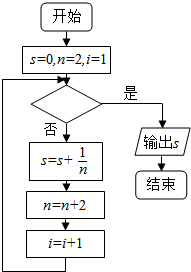
 如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个流程图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个流程图,其中判断框内应填入的条件是( )| A. | i≤21 | B. | i≤11 | C. | i≥21 | D. | i≥11 |
分析 由题意可知,首先是判断框中的条件不满足,所以框图依次执行循环,框图执行第一次循环后,S的值为$\frac{1}{2}$,执行第二次循环后,S的值为前2项的和,满足S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$,此时i的值为11,判断框中的条件应该满足,算法结束,由此得到判断框中的条件.
解答 解:框图首先给累加变量S赋值为0,n赋值2,给循环变量i赋值1.
此时判断框中的条件不满足,执行S=0+$\frac{1}{2}$,n=2+2=4,i=1+1=2;
此时判断框中的条件不满足,执行S=0+$\frac{1}{2}$+$\frac{1}{4}$,n=4+2=6,i=2+1=3;
此时判断框中的条件不满足,执行S=0+$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$,n=6+2=8,i=3+1=4;
…
此时判断框中的条件不满足,执行S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{18}$,n=18+2=20,i=9+1=10;
此时判断框中的条件不满足,执行S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$,n=18+2=22,i=10+1=11;
此时判断框中的条件满足,
故判断框内应填入的一个条件为i≥11.
故选:D.
点评 本题考查了循环结构,是直到型循环,区别当型和直到型的关键在于是满足条件执行循环还是不满足条件执行循环,满足条件执行循环的是当型结构,不满足条件执行循环的是直到型结构,是基础题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 8 | C. | 24 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\widehat{y}$=1.04x+2 | B. | $\widehat{y}$=1.04x+1.9 | C. | $\widehat{y}$=1.05x+1.9 | D. | $\widehat{y}$=1.9x+1.04 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com