练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在平面几何里，已知直角三角形ABC中，角C为 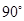，AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论：

    有三角形的勾股定理，给出空间中三棱锥的有关结论：________

    若三角形ABC的外接圆的半径为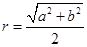，给出空间中三棱锥的有关结论：________

     

    【答案】

    在三棱锥O-ABC中，若三个侧面两两垂直，则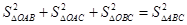；在三棱锥O-ABC中，若三个侧面两两垂直，且三条侧棱长分别为a,b,c,则其外接球的半径为

    【解析】

    试题分析：平面几何图形边长满足长度关系式，类比立体几何图形面积满足一定关系式，三角形中同一点出发的两线垂直，类比立体几何中同一条棱出发的三面互相垂直，直角三角形三边的平方关系类比立体几何中的三面平方关系得关系式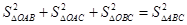

    直角三角形外接圆半径与两直角边有关系式，类比立体几何棱锥外接球半径与互相垂直的三条棱有关系式

    考点：知识的类比迁移能力

    点评：比较已知中给定的条件与所要类比的问题，找到他们之间的类似点，采用已知中的关系式形式类比写出所求的关系式

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2011•新疆模拟）在平面几何里，已知Rt△SAB的两边SA，SB互相垂直，且SA=a，SB=b，则AB边上的高h=
    ab
    		a2+b2
    ；现在把结论类比到空间：三棱锥S-ABC的三条侧棱SA，SB，SC两两相互垂直，SH⊥平面ABC，且SA=a，SB=b，SC=c，则点S到平面ABC的距离h'=
    abc
    		a2b2+b2c2+c2a2
    abc
    		a2b2+b2c2+c2a2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面几何里，已知直角三角形ABC中，角C为90°，AC=b，BC=a，运用类比方法探求空间中三棱锥的有关结论：
    有三角形的勾股定理，给出空间中三棱锥的有关结论：
    在三棱锥O-ABC中，若三个侧面两两垂直，则
    S
    2
    △OAB
    +
    S
    2
    △OAC
    +
    S
    2
    △OBC
    =
    S
    2
    △ABC
    在三棱锥O-ABC中，若三个侧面两两垂直，则
    S
    2
    △OAB
    +
    S
    2
    △OAC
    +
    S
    2
    △OBC
    =
    S
    2
    △ABC

    若三角形ABC的外接圆的半径为r=
    		a2+b2
    2
    ，给出空间中三棱锥的有关结论：
    在三棱锥O-ABC中，若三个侧面两两垂直，且三条侧棱长分别为a，b，c，则其外接球的半径为r=
    		a2+b2+c2
    2
    在三棱锥O-ABC中，若三个侧面两两垂直，且三条侧棱长分别为a，b，c，则其外接球的半径为r=
    		a2+b2+c2
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源：2014届海南琼海嘉积中学高二上教学监测（三）理科数学试卷（解析版） 题型：填空题

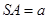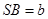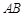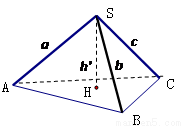
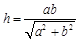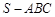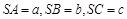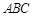    在平面几何里，已知直角△SAB的两边SA，SB互相垂直，且，则边上的高； 拓展到空间，如图，三棱锥的三条侧棱SB、SB、SC两两相互垂直,且,则点到面的距离

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    在平面几何里，已知直角三角形ABC中，角C为90°，AC=b，BC=a，运用类比方法探求空间中三棱锥的有关结论：
    有三角形的勾股定理，给出空间中三棱锥的有关结论：________
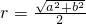    若三角形ABC的外接圆的半径为数学公式，给出空间中三棱锥的有关结论：________．

    查看答案和解析>>

    同步练习册答案