Question

11．如图所示，已知A、B、C是长轴为4的椭圆E上的三点，点A是长轴的一个端点，BC过椭圆中心O，且AC⊥BC，|BC|=2|AC|．
（1）求椭圆E的方程；
（2）设P为椭圆E上异于其顶点的任一点，以OP为直径的圆与圆x²+y²=$\frac{4}{3}$相交于点M、N，若直线MN在x轴、y轴上的截距分别为m、n，证明：$\frac{1}{3{m}^{2}}$+$\frac{1}{{n}^{2}}$为定值．

Answer 1

分析 （1）椭圆的长半轴长a=2，推出A（2，0），设椭圆E的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1，由椭圆的对称性知|OC|=|OB|，通过条件推出△AOC为等腰直角三角形，将C的坐标（1，1）代入椭圆方程得b椭圆E的方程；
（2）设点P（x₁，y₁），由OM⊥MP，ON⊥NP，推出圆的方程，过椭圆E上异于其顶点的任一点P，求得OP为直径的圆的方程，与⊙O：x²+y²=$\frac{4}{3}$相减可得直线MN的方程，求出直线MN在x轴、y轴上的截距分别为m、n，然后证明：$\frac{1}{3{m}^{2}}$+$\frac{1}{{n}^{2}}$为定值．

解答 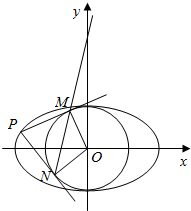解：（1）依题意知：椭圆的长半轴长a=2，则A（2，0），
设椭圆E的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1，
由椭圆的对称性知|OC|=|OB|，
又∵|BC|=2|AC|，AC⊥BC，
即有|OC|=|AC|∴△AOC为等腰直角三角形，
∴点C的坐标为（1，1），点B的坐标为（-1，-1），
将C的坐标（1，1）代入椭圆方程得b²=$\frac{4}{3}$，
∴所求的椭圆E的方程为$\frac{{x}^{2}}{4}$+$\frac{{3y}^{2}}{4}$=1；
（2）证明：设点P（x₁，y₁），由OM⊥MP，ON⊥NP，
∴O、M、P、N四点在同一圆上，
且圆的直径为OP，则圆心为（$\frac{{x}_{1}}{2}$，$\frac{{y}_{1}}{2}$），
其方程为（x-$\frac{{x}_{1}}{2}$）²+（y-$\frac{{y}_{1}}{2}$）²=$\frac{{{x}_{1}}^{2}+{{y}_{1}}^{2}}{4}$，
即x²+y²-x₁x-y₁y=0-----①
即点M、N满足方程①，又点M、N都在⊙O上，
∴M、N坐标也满足方程⊙O：x²+y²=$\frac{4}{3}$---------------②
②-①得直线MN的方程为x₁x+y₁y=$\frac{4}{3}$，
令y=0得m=$\frac{4}{3{x}_{1}}$，令x=0得n=$\frac{4}{3{y}_{1}}$，
∴x₁=$\frac{4}{3m}$，y₁=$\frac{4}{3n}$，又点P在椭圆E上，
∴（$\frac{4}{3m}$）²+3（$\frac{4}{3n}$）²=4，
即$\frac{1}{3{m}^{2}}$+$\frac{1}{{n}^{2}}$=$\frac{3}{4}$为定值．

点评 本题考查椭圆标准方程的求法，直线与椭圆的位置关系的应用，考查分析问题解决问题的能力，过定点问题的解题策略．