
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,第四日行二十四,几朝才得到其关,请公仔细算相还.”其大意为:“有一个人要走378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,其中第四天走了24里.”问此人( )天后到达目的地.
A.4B.5C.6D.8
科目:高中数学 来源: 题型:
【题目】记抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 在抛物线上,
在抛物线上,![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,直线
,直线![]() 的斜率都存在,且
的斜率都存在,且![]() ;探究:直线
;探究:直线![]() 是否过定点,若是,求出定点坐标;若不是,请说明理由.
是否过定点,若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,在点
,在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)已知![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)对于在![]() 中的任意一个常数
中的任意一个常数![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() ,请说明理由。
,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①在线性回归模型中,相关指数![]() 越接近于1,表示回归效果越好;
越接近于1,表示回归效果越好;
②两个变量相关性越强,则相关系数r就越接近于1;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均减少0.5个单位;
平均减少0.5个单位;
④两个模型中残差平方和越小的模型拟合的效果越好.
⑤回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
⑥若![]() 的观测值满足
的观测值满足![]() ≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
⑦从统计量中得知有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误. 其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项的和为
项的和为![]() ,公差
,公差![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,![]() ;数列
;数列![]() 满足:对于任意的
满足:对于任意的![]() ,等式
,等式![]() 都成立.
都成立.
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等比数列;
是等比数列;
(3)若数列![]() 满足
满足![]() ,试问是否存在正整数
,试问是否存在正整数![]() ,
,![]() (其中
(其中![]() ),使
),使![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一般来说,一个人脚掌越长,他的身高就越高.现对10名成年人的脚掌长![]() 与身高
与身高![]() 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为![]() )作为样本如下表所示.
)作为样本如下表所示.
脚掌长(x) | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
身高(y) | 141 | 146 | 154 | 160 | 169 | 176 | 181 | 188 | 197 | 203 |
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,作出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程![]() ;
;
(2)若某人的脚掌长为![]() ,试估计此人的身高;
,试估计此人的身高;
(3)在样本中,从身高180cm以上的4人中随机抽取2人作进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,圆
,圆![]() :
:![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(![]() ) 求直线
) 求直线![]() 的方程;
的方程;
(![]() )求直线
)求直线![]() 的斜率
的斜率![]() 的取值范围;
的取值范围;
(Ⅲ)是否存在过点![]() 且垂直平分弦
且垂直平分弦![]() 的直线
的直线![]() ?若存在,求直线
?若存在,求直线![]() 斜率
斜率![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于![]() 的偶数可以表示为两个素数的和”,如
的偶数可以表示为两个素数的和”,如![]() .现从不超过
.现从不超过![]() 的素数中,随机选取两个不同的数(两个数无序).(注:不超过
的素数中,随机选取两个不同的数(两个数无序).(注:不超过![]() 的素数有
的素数有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(1)列举出满足条件的所有基本事件;
(2)求“选取的两个数之和等于![]() ”事件发生的概率.
”事件发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查某社区80个人,以研究这一社区居民在晚上8点至十点时间段的休闲方式与性别的关系,得到下面的数据表:

(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,求这3人中至少有1人是以看书为休闲方式的概率;
(2)根据以上数据,能否有99%的把握认为“在晚上8点至十点时间段的休闲方式与性别有关系?”
参考公式: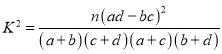 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com