
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)若![]() 的定义域为
的定义域为![]() ,判断
,判断![]() 的单调性,并加以说明;
的单调性,并加以说明;
(2)当![]() 时,是否存在
时,是否存在![]() ,
,![]() ,使得
,使得![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,若存在,求
,若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
科目:高中数学 来源: 题型:
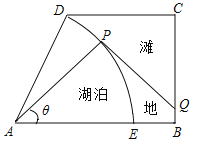
【题目】如图,某湿地公园的鸟瞰图是一个直角梯形,其中:![]() ,
,![]() ,
,![]() ,
,![]() 长1千米,
长1千米,![]() 长
长![]() 千米,公园内有一个形状是扇形的天然湖泊
千米,公园内有一个形状是扇形的天然湖泊![]() ,扇形
,扇形![]() 以
以![]() 长为半径,弧
长为半径,弧![]() 为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段
为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段![]() 线段
线段![]() 弧
弧![]() ,其中Q在线段
,其中Q在线段![]() 上(异于线段端点),
上(异于线段端点),![]() 与弧
与弧![]() 相切于P点(异于弧端点]根据市场行情
相切于P点(异于弧端点]根据市场行情![]() ,
,![]() 段的建造费用是每千米10万元,湖岸段弧
段的建造费用是每千米10万元,湖岸段弧![]() 的建造费用是每千米
的建造费用是每千米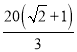 万元(步行道的宽度不计),设
万元(步行道的宽度不计),设![]() 为
为![]() 弧度观光步行道的建造费用为
弧度观光步行道的建造费用为![]() 万元.
万元.
(1)求步行道的建造费用![]() 关于
关于![]() 的函数关系式,并求其走义域;
的函数关系式,并求其走义域;
(2)当![]() 为何值时,步行道的建造费用最低?
为何值时,步行道的建造费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
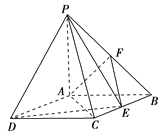
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有![]() ;
;
(3)当![]() 为何值时,
为何值时,![]() 与平面
与平面![]() 所成角的大小为45°.
所成角的大小为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
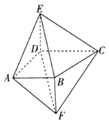
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,![]() ,
,![]() //
//![]() ,
,![]() .
.
(1)证明:![]() //平面BCE.
//平面BCE.
(2)设平面ABF与平面CDF所成的二面角为θ,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门共有员工60人,为调查他们的睡眠情况,逦过分层抽样获得12名员工每天睡眠的时间,数据如下表(单位:小时)
甲部门 | 6 | 7 | 8 | ||
乙部门 | 6 | 6.5 | 7 | 7.5 | |
丙部门 | 5.5 | 6 | 6.5 | 7 | 8.5 |
(1)求该单位乙部门的员工人数;
(2)若将每天睡眠时间不少于7小时视为睡眠充足,现从该单位任抽取1人,估计抽到的此人为睡眠充足者的概率;
(3)从甲部门和乙部门抽出的员工中,各随机选取一人,甲部门选出的员工记为A,乙部门选出的员工记为B.假设所有员工睡眠的时间相互独立.求A的睡眠时间不少于B的睡眠时间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|﹣a.
(1)当a=1时,解不等式f(x)>x+1;
(2)若存在实数x,使得f(x)![]() f(x+1),求实数a的取值范围.
f(x+1),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2019年11月1日到11月20日,某地区甲流疫情新增数据的走势图.
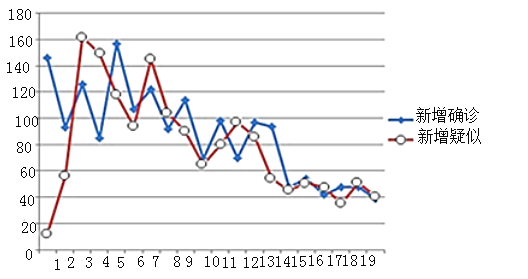
(1)从这20天中任选1天,求新增确诊和新增疑似的人数都超过100的概率;
(2)从新增确诊的人数超过100的日期中任选两天,用X表示新增确诊的人数超过140的天数,求X的分布列和数学期望;
(3)根据这20天统计数据,预测今后该地区甲流疫情的发展趋势.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集.整理、描述和分析.下面给出了部分信息:
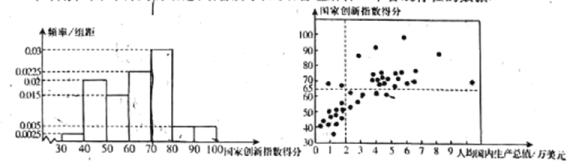
a.国家创新指数得分的频率分布直方图(数据分成7组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
b.国家创新指数得分在![]() 这一组的是:61.7,62.4,63.6,65.9,66.4,68.5,69.1,69.3,69.5.
这一组的是:61.7,62.4,63.6,65.9,66.4,68.5,69.1,69.3,69.5.
c.40个国家的人均国内生产总值(万美元)和国家创新指数得分情况统计图:
d.中国的国家创新指数得分为69.5,人均国内生产总值9960美元.
(以上数据来源于《国家创新指数报告(2018)》)
根据以上信息,解答下列问题:
(1)中国的国家创新指数得分排名世界第几?
(2)是否有99.9%的把握认为“人均国内生产总值影响国家创新指数得分”?
(3)用(1)(2)得到的结论,结合所学知识.合理解释d中客观存在的数据.
附: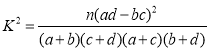 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com