
 已知下列三角形数表假设第行的第二个数为an(n≥2,n∈N*).
已知下列三角形数表假设第行的第二个数为an(n≥2,n∈N*).分析 (1)每行的第一个数为所在的行数,从第二项起,每个元素为上行两个相邻元素的和,即可求得第六行的所有数字;
(2)由题意可知an+1=an+n(n≥2),a2=2,则an-an-1=n-1(n≥3),累加即可求得an,当n=2时,${a_2}=\frac{1}{2}×{2^2}-\frac{1}{2}×2+1\;\;=2$,也满足上述等式,即可求得an的通项公式;
(3)由题意可知:${b_n}=\frac{2}{{{n^2}-n+2}}<\frac{2}{{{n^2}-n}}=2(\frac{1}{n-1}-\frac{1}{n})$,采用“裂项法”即可求得b1+b2+b3+…+bn=2(1-$\frac{1}{n}$)$2(1-\frac{1}{n})<2$<2.
解答 解:(1)第六行的所有6个数字分别是6,16,25,25,16,6;--------(2分)
(2)依题意an+1=an+n(n≥2),a2=2---(4分)
an-an-1=n-1(n≥3),
a3-a2=2an=a2+(a3-a2)+(a4-a3)+…+(an-an-1),
=$2+2+3+…+(n-1)=2+\frac{(n-2)(n+1)}{2}$,
∴${a_n}=\frac{1}{2}{n^2}-\frac{1}{2}n+1\;\;\;(n≥3)$;-------(7分)
当n=2时,${a_2}=\frac{1}{2}×{2^2}-\frac{1}{2}×2+1\;\;=2$,
也满足上述等式
所以${a_n}=\frac{1}{2}{n^2}-\frac{1}{2}n+1\;\;\;(n≥2)$-------(8分)
(3)证明:因为anbn=1,则${b_n}=\frac{2}{{{n^2}-n+2}}<\frac{2}{{{n^2}-n}}=2(\frac{1}{n-1}-\frac{1}{n})$-------(11分)
${b_2}+{b_3}+{b_4}+…+{b_n}<2[(\frac{1}{1}-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+…+(\frac{1}{n-1}-\frac{1}{n})]$=$2(1-\frac{1}{n})<2$,
∴b1+b2+b3+…+bn<2.--(12分)
点评 本题考查数列的综合应用,考查数列通项公式的求法,“裂项法”求数列的前n项和,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
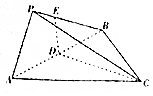 如图所示,三棱锥P-ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA=$\frac{3}{2}$,PB=$\frac{3\sqrt{3}}{2}$,则三棱锥P-ABC的外接球的表面积为13π.
如图所示,三棱锥P-ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA=$\frac{3}{2}$,PB=$\frac{3\sqrt{3}}{2}$,则三棱锥P-ABC的外接球的表面积为13π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知MOD函数是一个求余函数,记MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2.如图是某个算法的程序框图,若输入m的值为48时,则输出i的值为( )
已知MOD函数是一个求余函数,记MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2.如图是某个算法的程序框图,若输入m的值为48时,则输出i的值为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com