
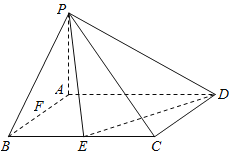
【题目】在四棱锥![]() 中,底面ABCD是矩形,
中,底面ABCD是矩形,![]() 平面ABCD,
平面ABCD,![]() ,E,F是线段BC,AB的中点.
,E,F是线段BC,AB的中点.
![]() Ⅰ
Ⅰ![]() 证明:
证明:![]() ;
;
![]() Ⅱ
Ⅱ![]() 在线段PA上确定点G,使得
在线段PA上确定点G,使得![]() 平面PED,请说明理由.
平面PED,请说明理由.
科目:高中数学 来源: 题型:
【题目】为研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:![]() )的分组区间为
)的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
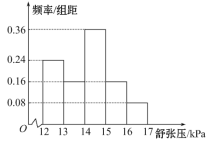
,![]() ,将其按从左到右的顺序分别编号为第一组,第二组,......,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有
,将其按从左到右的顺序分别编号为第一组,第二组,......,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有![]() 人,第三组中没有疗效的有
人,第三组中没有疗效的有![]() 人,则第三组中有疗效的人数为( )
人,则第三组中有疗效的人数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列等式:12=1,12﹣22=﹣3,12﹣22+32=6,12﹣22+32﹣42=﹣10,…由以上等式推测到一个一般的结论:对于n∈N* , 12﹣22+32﹣42+…+(﹣1)n+1n2= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则,将某些整数染成红色,先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,…,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,……,则在这个红色子数列中,由1开始的第2019个数是( )
A. 3972 B. 3974 C. 3991 D. 3993
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() 点
点![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() (
(![]() 为实数).
为实数).

(1)求二面角![]() 的余弦值;
的余弦值;
(2)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(3)求证:直线![]() 与直线
与直线![]() 不可能垂直.
不可能垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
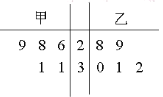
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张三同学从每年生日时对自己的身高测量后记录如表:
![]()
(附:回归直线的斜率和截距的最小二乘法估计公式分别为: ,
,![]() )
)
(1)求身高![]() 关于年龄
关于年龄![]() 的线性回归方程;(可能会用到的数据:
的线性回归方程;(可能会用到的数据:![]() (cm))
(cm))
(2)利用(1)中的线性回归方程,分析张三同学![]() 岁起到
岁起到![]() 岁身高的变化情况,如
岁身高的变化情况,如 ![]() 岁之前都符合这一变化,请预测张三同学
岁之前都符合这一变化,请预测张三同学 ![]() 岁时的身高。
岁时的身高。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com