练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝3x，且f(a＋2)＝18，g(x)＝3ax－4x的定义域为区间[－1,1]．

    (1)求g(x)的解析式；

    (2)判断g(x)的单调性．

     

    【答案】

    (1)∵f(a＋2)＝18，f(x)＝3x.

    ∴3a＋2＝18，即3a＝2.

    故g(x)＝(3a)x－4x＝2x－4x，x∈[－1,1]．

    (2)g(x)＝－(2x)2＋2x＝－2＋.

    当x∈[－1,1]时，2x∈.令t＝2x，

    由二次函数单调性得

    －2＋在上是减函数，

    ∴函数g(x)在[－1,1]上是减函数．

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013届浙江省临海市白云高级中学高三第三次模拟理科数学试卷（带解析） 题型：解答题

    已知函数f (x)＝3 sin2 ax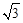＋sin ax cos ax＋2 cos2 ax的周期为π，其中a＞0．
    (Ⅰ) 求a的值；
    (Ⅱ) 求f (x)的值域．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省临海市高三第三次模拟理科数学试卷（解析版） 题型：解答题

    已知函数f (x)＝3 sin2 ax＋sin ax cos ax＋2 cos2 ax的周期为π，其中a＞0．

    (Ⅰ) 求a的值；

    (Ⅱ) 求f (x)的值域．

     

    查看答案和解析>>

    科目：高中数学 来源：2014届江苏省高二下学期期中考试文科数学试卷（解析版） 题型：解答题

    已知函数f(x)＝3－2log2x，g(x)＝log2x.

    (1)如果x∈[1,4]，求函数h(x)＝(f(x)＋1)g(x)的值域；

    (2)求函数M(x)＝的最大值；

    (3)如果不等式f(x2)f()>kg(x)对x∈[2,4]有解，求实数k的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省高三高考模拟测试理科数学试卷（解析版） 题型：解答题

    已知函数f (x)＝3 sin2 ax＋sin ax cos ax＋2 cos2 ax的周期为π，其中a＞0．

    (Ⅰ) 求a的值；

    (Ⅱ) 求f (x)的值域．

     

    查看答案和解析>>

    科目：高中数学 来源：2012年人教A版高中数学必修1单调性与最大（小）值练习卷（二）（解析版） 题型：选择题

    已知函数f(x)＝3－2|x|，g(x)＝x2－2x，构造函数F(x)，定义如下：当f(x)≥g(x)时，F(x)＝g(x)；当f(x)<g(x)时，F(x)＝f(x)，那么F(x)(　　)

    A．有最大值3，最小值－1

    B．有最大值3，无最小值

    C．有最大值7－，无最小值

    D．无最大值，也无最小值

     

    查看答案和解析>>

    同步练习册答案