
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.求证: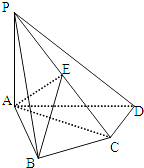
(Ⅰ)CD⊥AE;
(Ⅱ)PD⊥平面ABE.
【答案】证明:(Ⅰ)∵PA⊥底面ABCD,∴PA⊥CD,又AC⊥CD,PA∩AC=A,
故CD⊥平面PAC.
又AE平面PAC,∴CD⊥AE.
(Ⅱ)由题意:AB⊥AD,
∴AB⊥平面PAD,从而AB⊥PD.
又AB=BC,且∠ABC=60°,
∴AC=AB,从而AC=PA.
又E为PC之中点,∴AE⊥PC.
由(Ⅰ)知:AE⊥CD,∴AE⊥平面PCD,从而AE⊥PD.
又AB∩AE=A,
故PD⊥平面ABE

【解析】(1)根据题意结合已知条件利用线面垂直的性质定理得到线线垂直再结合线面垂直的判定定理即可得出结论。(2)利用已知的线面垂直得出线线垂直再结合(1)的结论由线面垂直的判定定理即可得证。


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图: 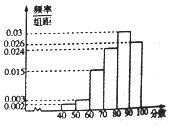
(I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于60分的市民中随机抽取2人进行座谈,求这2人评分恰好都在[50,60)的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数= ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a、b、c分别是△ABC的三个内角A、B、C的对边.
(1)若△ABC面积S△ABC= ![]() ,c=2,A=60°,求a、b的值;
,c=2,A=60°,求a、b的值;
(2)若a=ccosB,且b=csinA,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的是( )
A.斜率相等的两条直线一定平行
B.若两条不重合的直线l1 , l2平行,则它们的斜率一定相等
C.直线l1:x=1与直线l2:x=2不平行
D.直线l1:( ![]() -1)x+y=2与直线l2:x+(
-1)x+y=2与直线l2:x+( ![]() +1)y=3平行
+1)y=3平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(-1,1),B(1,1),C(2, ![]() +1),
+1),
(1)求直线AB和AC的斜率.
(2)若点D在线段AB(包括端点)上移动时,求直线CD的斜率的变化范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥 ![]() 中,
中, ![]() 平面
平面 ![]() ,
, ![]() ∥
∥ ![]() ,
, ![]() ,
,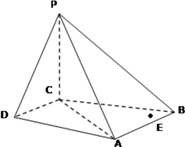
(1)求证: ![]() 平面
平面 ![]()
(2)求证:平面 ![]() 平面
平面 ![]()
(3)设点 ![]() 为
为 ![]() 中点,在棱
中点,在棱 ![]() 上是否存在点
上是否存在点 ![]() ,使得
,使得 ![]() ∥平面
∥平面 ![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,a1=2,前n项和为Sn , 若数列{an+1}也是等比数列,则Sn等于( ).
A.2n+1-2
B.3n
C.2n
D.3n-1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为 ![]() ,右焦点为(
,右焦点为( ![]() ,0)
,0)
(1)求椭圆C的方程;
(2)若过原点 ![]() 作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值.
作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(x0 , y0)在x2+y2=r2(r>0)外,则直线x0x+y0y=r2与圆x2+y2=r2的位置关系为( )
A.相交
B.相切
C.相离
D.相交、相切、相离三种情况均有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com