
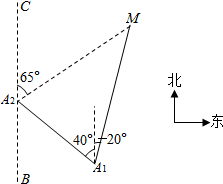
 如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里.
如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里. 科目:高中数学 来源: 题型:解答题
 如图所示,在矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2$\sqrt{3}$,O,H分别为AE,AB的中点,平面BDE∩面DOH=l.
如图所示,在矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2$\sqrt{3}$,O,H分别为AE,AB的中点,平面BDE∩面DOH=l.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |x-a|≤3a | B. | |x-a|<3a | C. | |x-a|<0.03a | D. | |x-a|≤0.03a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-5)∪[-4,+∞) | B. | (-5,-4] | C. | (-∞,-4] | D. | [-4,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
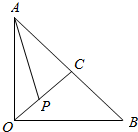 如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$.
如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com