
 中,四边形
中,四边形 为矩形,
为矩形, 为等腰三角形,
为等腰三角形, ,平面
,平面 平面
平面 ,且
,且 ,
, 分别为
分别为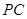 和
和 的中点.
的中点.
 平面
平面 ;
; 平面
平面 ;
; 的体积.
的体积.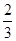 .
.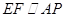 从而达到目标;(Ⅱ)要证面面垂直,由面面垂直的判定定理知可先考察线面垂直,要证线面垂直,又要先考察线线垂直;(Ⅲ)求棱锥的体积,关键是作出其高,由面
从而达到目标;(Ⅱ)要证面面垂直,由面面垂直的判定定理知可先考察线面垂直,要证线面垂直,又要先考察线线垂直;(Ⅲ)求棱锥的体积,关键是作出其高,由面 面
面 及
及 为等腰直角三角形,易知
为等腰直角三角形,易知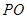 (
( 中点为
中点为 ),就是其高,问题得以解决.
),就是其高,问题得以解决.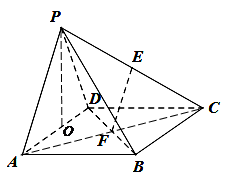
 .
. 为矩形且
为矩形且 是
是 的中点.∴
的中点.∴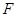 也是
也是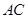 的中点.
的中点.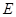 是
是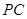 的中点,
的中点,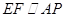 2分
2分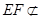 平面
平面 ,
,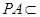 平面
平面 ,所以
,所以 平面
平面 ; 4分
; 4分 平面
平面 ,
,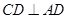 ,平面
,平面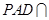 平面
平面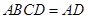 ,
,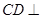 平面
平面 ,又
,又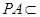 平面
平面 ,所以
,所以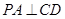 6分
6分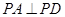 ,
,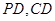 是相交直线,所以
是相交直线,所以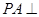 面
面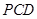
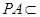 平面
平面 ,平面
,平面 平面
平面 ; 8分
; 8分 中点为
中点为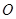 .连结
.连结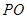 ,
, 为等腰直角三角形,所以
为等腰直角三角形,所以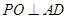 ,
, 面
面 且面
且面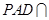 面
面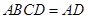 ,
,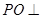 面
面 ,
,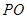 为四棱锥
为四棱锥 的高.
的高.  10分
10分 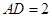 得
得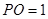 .又
.又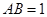 .
. 的体积
的体积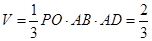 12分
12分

 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源:不详 题型:解答题
 ,?O的直径AB=2, C为弧AB的中点,D为AC的中点.
,?O的直径AB=2, C为弧AB的中点,D为AC的中点.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.若l∥α,l∥β,则α∥β |
| B.若l∥α,l⊥β,则α⊥β |
| C.若α⊥β,l⊥α,则l⊥β |
| D.若α⊥β,l∥α,则l⊥β |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 且
且 .给出下列命题:
.给出下列命题: 且
且 ;
; 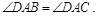
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com