
【题目】甲、乙两人投篮命中的概率分别为![]() 与
与![]() ,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
(1)求比赛结束后甲的进球数比乙的进球数多1的概率;
(2)设![]() 表示比赛结束后甲、乙两人进球数的差的绝对值,求
表示比赛结束后甲、乙两人进球数的差的绝对值,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某校高二100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() .
.
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若将频率视为概率,现从全市高二学生中随机查看5名学生的期中考试语文成绩,记成绩优秀(不低于80分)的学生人数为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象经过点(
的图象经过点(![]() ,
,![]() )和(
)和(![]() ,
,![]() ),完成下面问题:
),完成下面问题:

(1)求函数![]() 的表达式;
的表达式;
(2)在给出的平面直角坐标系中,请用适当的方法画出这个函数的图象,并写出这个函数的一条性质;
(3)已知函数![]() 的图象如图所示,结合你所画出
的图象如图所示,结合你所画出![]() 的图象,直接写出
的图象,直接写出![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了整顿道路交通秩序,某地考虑对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通人中随机抽取200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如下数据:
处罚金额 | 5 | 10 | 15 | 20 |
会闯红灯的人数 | 50 | 40 | 20 | 0 |
若用表中数据所得频率代替概率.
(1)当处罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(2)将选取的200人中会闯红灯的市民分为两类:![]() 类市民在罚金不超过10元时就会改正行为;
类市民在罚金不超过10元时就会改正行为;![]() 类是其它市民.现对
类是其它市民.现对![]() 类与
类与![]() 类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为
类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为![]() 类市民的概率是多少?
类市民的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查机构对某高科技行业进行调查统计,得到该行业从业者学历分布扇形图和从事该行业岗位分布条形图,如图所示,判断以下三种说法的正误:①该高科技行业从业人员中学历为博士的占一半以上;②该高科技行业中从事技术岗位的人数超过总数的30%;③该高科技行业中从事运营岗位的人员主要是本科生.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,![]() 平面ABCD,
平面ABCD,![]() .
.

(I)求证:![]() 平面ABCD;
平面ABCD;
(II)求证:平面ACF⊥平面BDF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部影片的盈利额(即影片的票房收入与固定成本之差)记为![]() ,观影人数记为
,观影人数记为![]() ,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后
,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后![]() 与
与![]() 的函数图象.
的函数图象.

给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是____________.(填写所有正确说法的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每当《我心永恒》这首感人唯美的歌曲回荡在我们耳边时,便会想起电影《泰坦尼克号》中一暮暮感人画面,让我们明白了什么是人类的“真、善、美”.为了推动我市旅游发展和带动全市经济,更为了向外界传递遂宁人民的“真、善、美”.我市某地将按“泰坦尼克号”原型![]() 比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市
比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
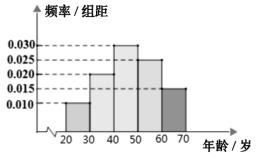
(1)求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄在
人,求所抽取的人中恰好没有年龄在![]() 段的概率.
段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将![]() 的方程化为普通方程,将
的方程化为普通方程,将![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数,且
为参数,且![]() ),
),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com