
【题目】已知函数f(x)=alnx+x2+bx+1在点(1,f(1))处的切线方程为4x﹣y﹣12=0.
(1)求函数f(x)的解析式;
(2)求f(x)的单调区间和极值.
【答案】
(1)解:求导f′(x)= ![]() +2x+b,由题意得:
+2x+b,由题意得:
f′(1)=4,f(1)=﹣8,
则 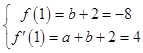 ,解得
,解得 ![]() ,
,
所以f(x)=12lnx+x2﹣10x+1
(2)解:f(x)定义域为(0,+∞),
f′(x)= ![]() ,
,
令f′(x)>0,解得:x<2或x>3,
所以f(x)在(0,2)递增,在(2,3)递减,在(3,+∞)递增,
故f(x)极大值=f(2)=12ln2﹣15,
f(x)极小值=f(3)=12ln3﹣20
【解析】(1)求出函数的导数,计算f′(1),f(1),得到关于a,b的方程组,求出a,b的值,从而求出f(x)的解析式即可;(2)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PC= ![]() AC,平面PAC⊥平面ABCD.
AC,平面PAC⊥平面ABCD. 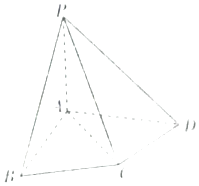
(1)点E在棱PC上,试确定点E的位置,使得PD⊥平面ABE;
(2)求二面角A﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某厂生产某种产品的过程中记录的几组数据,其中![]() 表示产量(单位:吨),
表示产量(单位:吨),![]() 表示生产中消耗的煤的数量(单位:吨).
表示生产中消耗的煤的数量(单位:吨).
|
|
|
|
|
|
|
|
|
|
|
|
(1)试在给出的坐标系下作出散点图,根据散点图判断,在![]() 与
与![]() 中,哪一个方程更适合作为变量
中,哪一个方程更适合作为变量![]() 关于
关于![]() 的回归方程模型?(给出判断即可,不需要说明理由)
的回归方程模型?(给出判断即可,不需要说明理由)
(2)根据(1)的结果以及表中数据,建立变量![]() 关于
关于![]() 的回归方程.并估计生产
的回归方程.并估计生产![]() 吨产品需要准备多少吨煤.参考公式:
吨产品需要准备多少吨煤.参考公式: .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:

其中=1,2,3,4,5,6,7.
(1)以每天进店人数为横轴,每天商品销售件数为纵轴,画出散点图;
(2)求线性回归方程;(结果保留到小数点后两位)
(参考数据:![]() =3 245,
=3 245, ![]() =25,
=25, ![]() =15.43,
=15.43, ![]() =5 075)
=5 075)
(3)预测进店人数为80人时,商品销售的件数.(结果保留整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a>0)的导函数y=f′(x)的两个零点为0和3.
(a>0)的导函数y=f′(x)的两个零点为0和3.
(1)求函数f(x)的单调递增区间;
(2)若函数f(x)的极大值为 ![]() ,求函数f(x)在区间[0,5]上的最小值.
,求函数f(x)在区间[0,5]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(﹣1)=0,当x>0时,xf′(x)﹣f(x)<0,则使得f(x)>0成立的x的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:

(1)求分数![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中.己知直线l的参数方程为  (t为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρ=4.
(t为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρ=4.
(1)写出直线l的普通方程与曲线C的直角坐标系方程;
(2)直线l与曲线C相交于A、B两点,求∠AOB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)经过点P(﹣2,0)与点(1,1).
=1(a>b>0)经过点P(﹣2,0)与点(1,1).
(1)求椭圆的方程;
(2)过P点作两条互相垂直的直线PA,PB,交椭圆于A,B.
①证明直线AB经过定点;
②求△ABP面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com